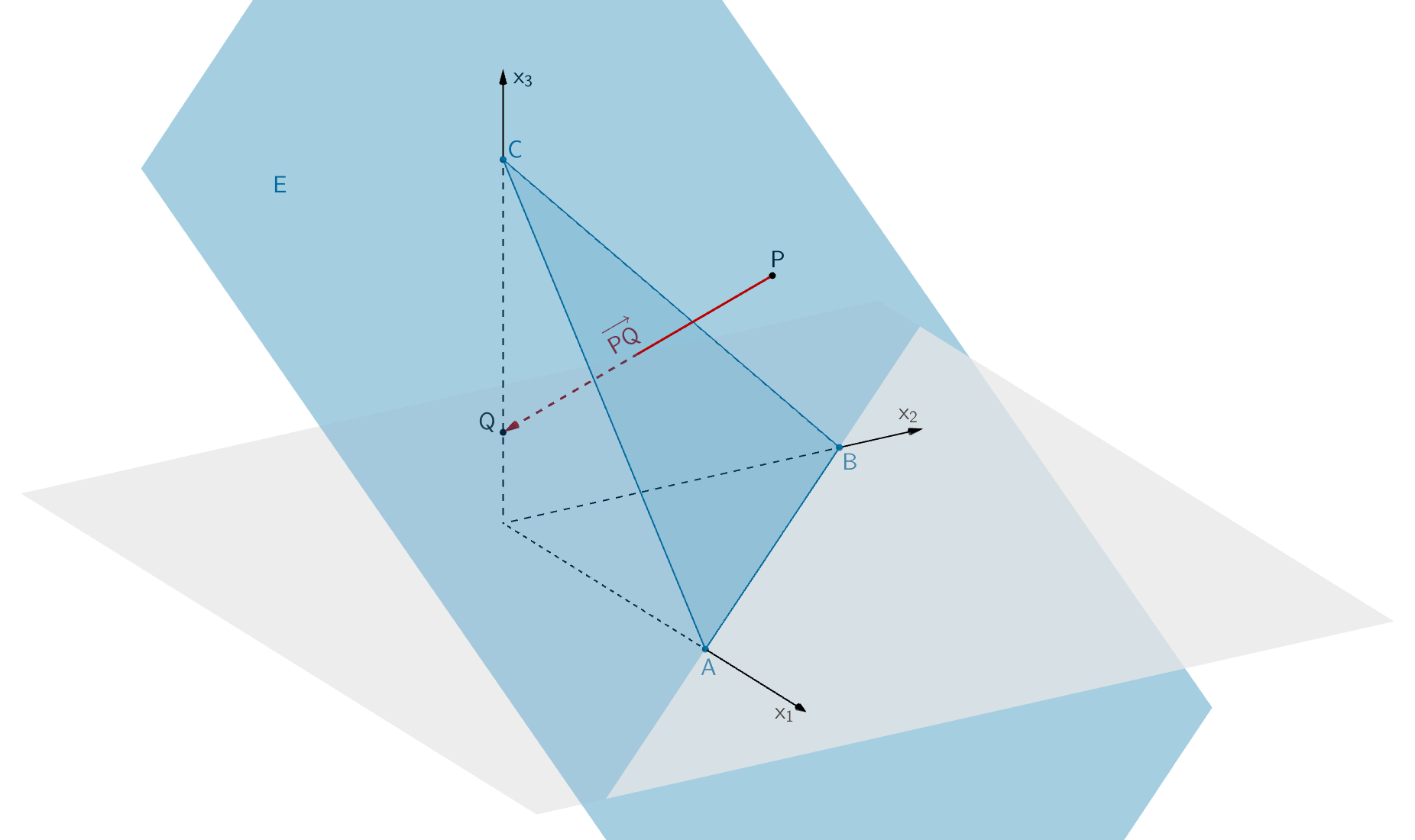
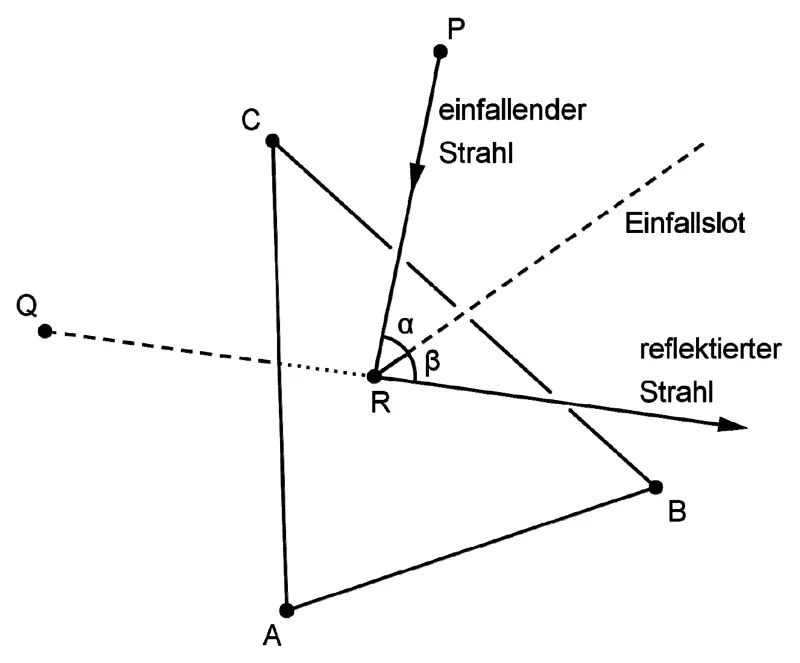
Der einfallende Lichtstrahl wird in demjenigen Punkt des Spiegels reflektiert, der im Modell durch den Punkt \(R\) dargestellt wird. Der reflektierte Lichtstrahl geht für einen Beobachter scheinbar von einer Lichtquelle aus, deren Position im Modell durch den Punkt \(Q\,(0|0|1)\) beschrieben wird (vgl. Abbildung).
Zeigen Sie, dass die Punkte \(P\) und \(Q\) bezüglich der Ebene \(E\) symmetrisch sind.
(3 BE)
Lösung zu Teilaufgabe c
Die Punkte \(P\) und \(Q\) sind bezüglich der Ebene \(E\) symmetrisch, wenn der Vektor \(\overrightarrow{PQ}\) zur Ebene \(E\) senkrecht ist und die Punkte \(P\) und \(Q\) den gleichen Abstand von der Ebene \(E\) haben.
\[\overrightarrow{PQ} \perp E \quad \Longrightarrow \quad \overrightarrow{PQ} = k \cdot \overrightarrow{n}_{E}\,; \enspace k \in \mathbb R\]
\[d\,(P;E) = d\,(Q;E)\]
bzw.
\[d\,(P;E) = \frac{1}{2} \cdot \overline{PQ}\]
Nachweisen, dass \(\overrightarrow{PQ} \perp E\) gilt:
\[E\,\colon\, x_1 + x_2 + x_3 = 4\,; \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\]
\[P\,(2|2|3)\,,\enspace Q\,(0|0|1)\]
\[\overrightarrow{PQ} = \overrightarrow{Q} - \overrightarrow{P} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \begin{pmatrix} 2 \\ 2 \\ 3 \end{pmatrix} = \begin{pmatrix} -2 \\ -2 \\ -2 \end{pmatrix} = (-2) \cdot \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}\]
\[\Longrightarrow \quad \overrightarrow{PQ} = (-2) \cdot \overrightarrow{n}_{E}\]
\[\Longrightarrow \quad \overrightarrow{PQ} \perp E\]
Abstand des Punktes \(P\) von der Ebene \(E\):
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
\[E\,\colon\, x_1 + x_2 + x_3 = 4\]
\[P\,(2|2|3)\]
Betrag des Normalenvektors der Ebene \(E\):
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \overrightarrow{n}_{E} \vert = \left| \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \right| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3}\]
\[E^{HNF}\,\colon\, \frac{x_1 + x_2 + x_3 - 4}{\sqrt{3}} = 0 \]
Abstände \(d\,(P;E)\) und \(d\,(Q;E)\) berechnen:
\[\begin{align*} d\,(P;E) &= \left| \frac{p_1 + p_2 + p_3 - 4}{\sqrt{3}} \right| \\[0.8em] &= \left| \frac{2 + 2 + 3 - 4}{\sqrt{3}} \right| \\[0.8em] &= \frac{3}{\sqrt{3}} = \sqrt{3} \end{align*}\]
\[\begin{align*} d\,(Q;E) &= \left| \frac{q_1 + q_2 + q_3 - 4}{\sqrt{3}} \right| \\[0.8em] &= \left| \frac{0 + 0 + 1 - 4}{\sqrt{3}} \right| \\[0.8em] &= \left| \frac{-3}{\sqrt{3}} \right| \\[0.8em] &= \frac{3}{\sqrt{3}} = \sqrt{3} \end{align*}\]
\[\Longrightarrow \quad d\,(p;E) = d\,(Q;E)\]
oder:
\[\vert \overrightarrow{PQ} \vert = \left| \begin{pmatrix} -2 \\ -2 \\ -2 \end{pmatrix} \right| = \sqrt{(-2)^2 + (-2)^2 + (-2)^2} = \sqrt{12} = 2\sqrt{3}\]
\[\Longrightarrow \quad d\,(P;E) = \frac{1}{2} \cdot \overline{PQ}\]
Folglich sind die Punkte \(P\) und \(Q\) bezüglich der Ebene \(E\) symmetrisch.