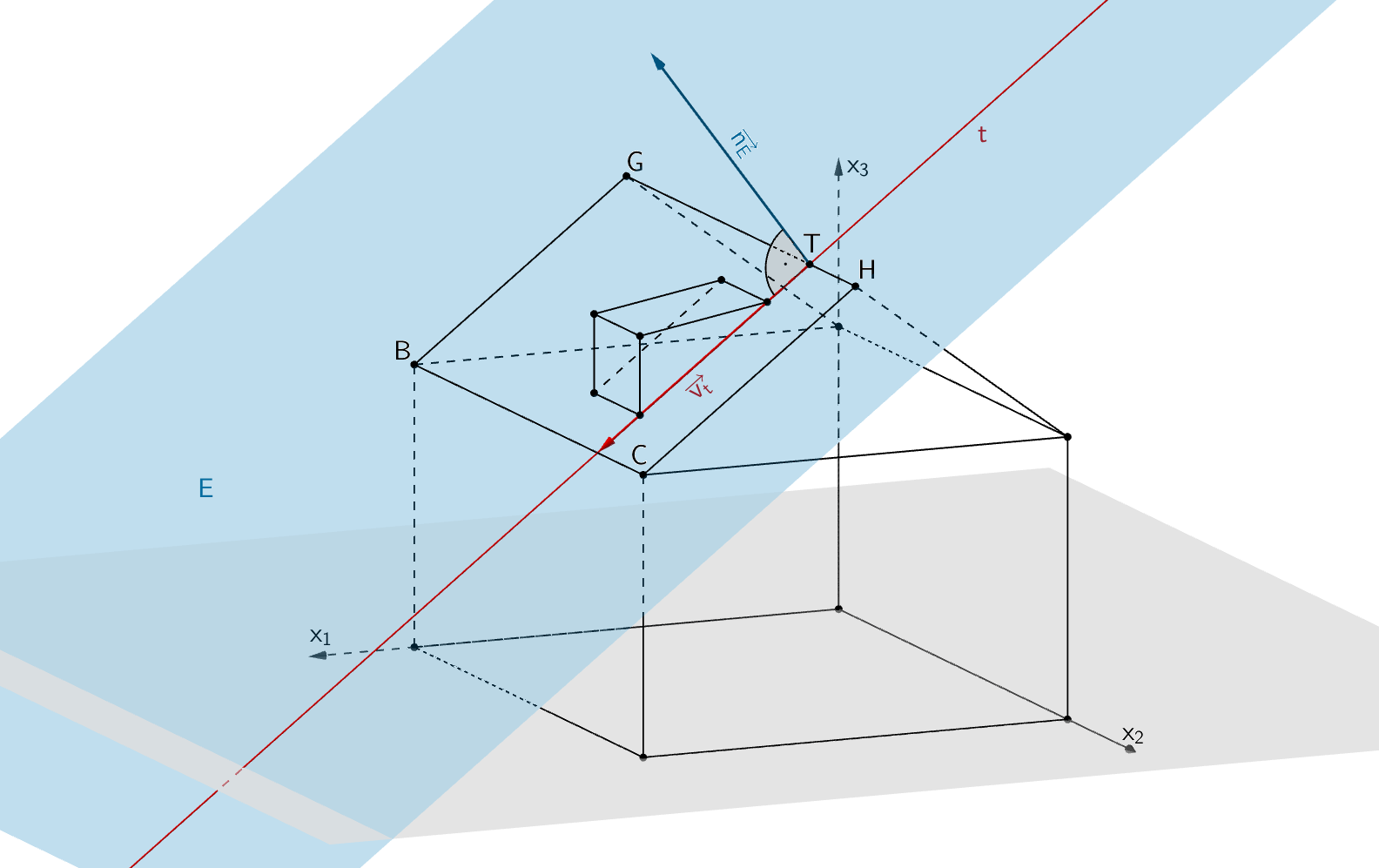
Die Dachfläche, auf der die Dachgaube errichtet wird, liegt im Modell in der Ebene \(E\,\colon\, 3x_1 + 4x_3 - 44 = 0\).
Die Dachgaube soll so errichtet werden, dass sie von dem seitlichen Rand der Dachfläche, der im Modell durch die Strecke \([HC]\) dargestellt wird, den Abstand 2 m und vom First des Dachs den Abstand 1 m hat. Zur Ermittlung der Koordinaten des Punkts \(M\) wird die durch den Punkt \(T\,(4|8|8)\) verlaufende Gerade \(\displaystyle t\,\colon\, \overrightarrow{X} = \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix}\), \(\lambda \in \mathbb R\), betrachtet.
Begründen Sie, dass \(t\) in der Ebene \(E\) verläuft und von der Geraden \(HC\) den Abstand 2 besitzt.
(5 BE)
Lösung zu Teilaufgabe c
Begründung, dass die Gerade \(t\) in der Ebene \(E\) liegt
1. Lösungsansatz: Orthogonale Vektoren
Die Gerade \(t\) liegt in der Ebene \(E\), wenn der Richtungsvektor \(\overrightarrow{v}_{t}\) der Geraden \(t\) senkrecht zum Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) ist.
Zudem liegt der Punkt \(T\) in der Ebene \(E\), da das Rechteck \(BCHG\) die Ebene \(E\) repräsentiert (siehe Teilaufgabe b) und der Punkt \(T\) auf der Strecke \([GH]\) liegt.
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
\[\overrightarrow{v}_{t} \circ \overrightarrow{n}_{E} = 0 \quad \Longleftrightarrow \quad \overrightarrow{v}_{t} \perp \overrightarrow{n}_{E} \]
\[t\,\colon\,\overrightarrow{X} = \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix} \quad \Longrightarrow \quad \overrightarrow{v}_{t} = \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix}\]
\[E\,\colon\, 3x_{1} + 4x_{3} - 44 = 0 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 3 \\ 0 \\ 4 \end{pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[\begin{align*} \overrightarrow{v}_{t} \circ \overrightarrow{n}_{E} &= 0 \\[0.8em] \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix} \circ \begin{pmatrix} 3 \\ 0 \\ 4 \end{pmatrix} &= 0 \\[0.8em] 4 \cdot 3 + 0 \cdot 0 + (-3) \cdot 4 &= 0 \\[0.8em] 0 &= 0 \quad (\text{w}) \end{align*}\]
\[\Longrightarrow \quad \overrightarrow{v}_{t} \perp \overrightarrow{n}_{E}\]
\[\Longrightarrow \quad t \subset E\]
2. Lösungsansatz: Parallele Vektoren
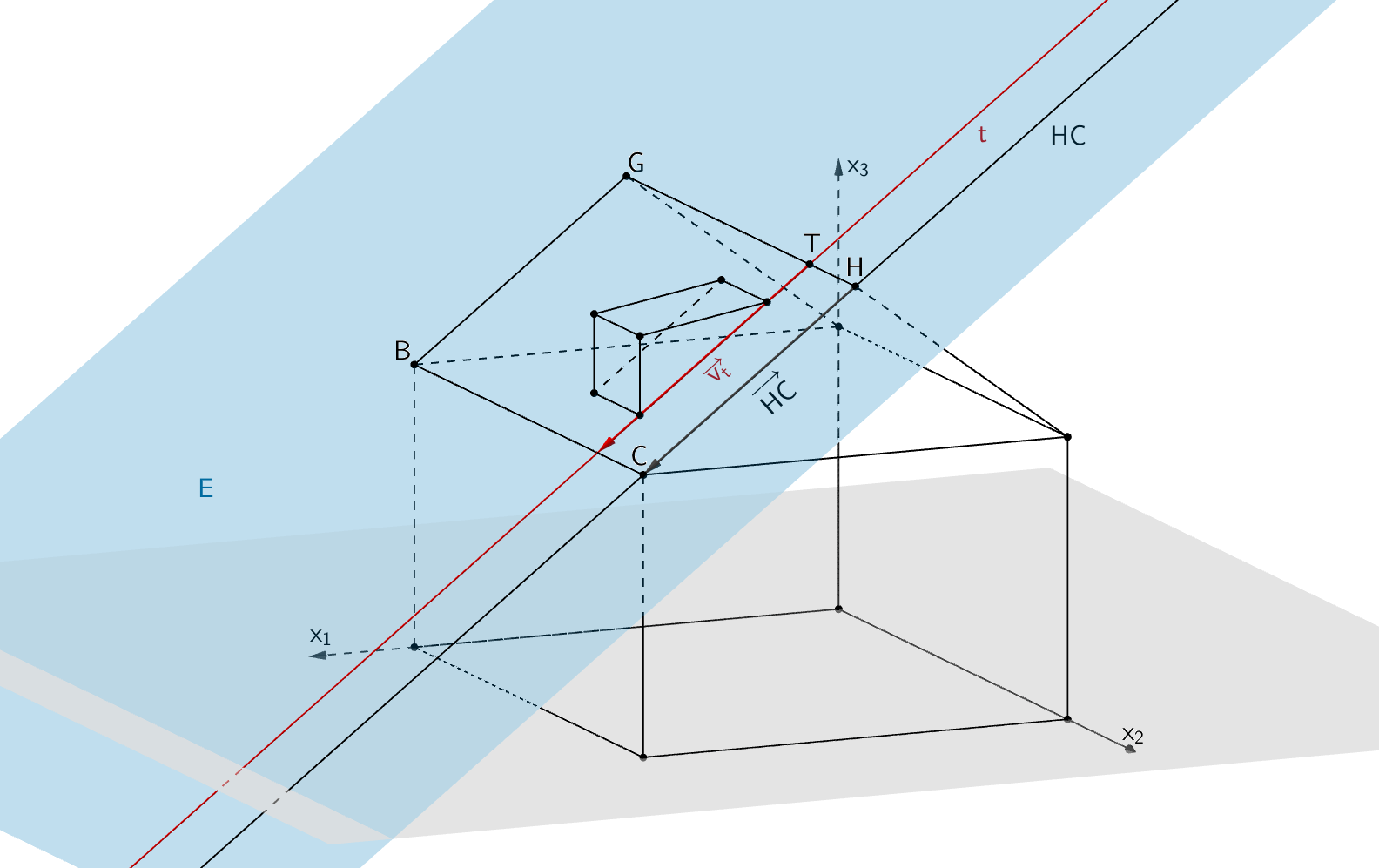
Die Gerade \(t\) liegt in der Ebene \(E\), wenn der Richtungsvektor \(\overrightarrow{v}_{t}\) der Geraden \(t\) parallel zum Vektor \(\overrightarrow{HC} \in E\) verläuft und der Punkt \(T\) in der Ebene \(E\) liegt.
Nachweisen, dass \(T \in E\) gilt:
Der Punkt \(T\) liegt in der Ebene \(E\), da das Rechteck \(BCHG\) die Ebene \(E\) repräsentiert (siehe Teilaufgabe b) und der Punkt \(T\) auf der Strecke \([GH]\) liegt.
\(\left. \begin{align*} BCGH \subset E& \\ T \in [GH]& \end{align*} \right\} \enspace \Rightarrow \enspace T \in E \)
oder:
\[E\,\colon\, 3x_{1} + 4x_{3} - 44 = 0\,; \quad T\,(4|8|8)\]
\[\begin{align*}T \in E\,\colon\, 3 \cdot 4 + 4 \cdot 8 - 44 &= 0 \\[0.8em] 12 + 32 - 44 &= 0 \\[0.8em] 0 &= 0 \quad (\text{w}) \end{align*}\]
\[\Longrightarrow \quad T \in E\]
Nachweisen, dass \(\overrightarrow{v_{t}} \parallel \overrightarrow{HC}\) gilt:
\[t\,\colon\,\overrightarrow{X} = \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix} \quad \Longrightarrow \quad \overrightarrow{v}_{t} = \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix}\]
\(H\,(4|10|8)\), \(C\,(8|10|5)\) (siehe Abbildung zur Aufgabengruppe)
\[\overrightarrow{HC} = \overrightarrow{C} - \overrightarrow{H} = \begin{pmatrix} 8 \\ 10 \\ 5 \end{pmatrix} - \begin{pmatrix} 4 \\ 10 \\ 8 \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \\ -3 \end{pmatrix} = \overrightarrow{v}_{t}\]
\[\Longrightarrow \quad \overrightarrow{v_{t}} \parallel \overrightarrow{HC}\]
\[\left. \begin{align*} T \in E& \\ \overrightarrow{v_{t}} \parallel \overrightarrow{HC}& \end{align*} \right\} \enspace \Rightarrow \enspace t \subset E\]
Nachweis, dass die Gerade \(t\) von der Geraden \(HC\) den Abstand 2 besitzt
Wie in Teilaufgabe a beschrieben, ist \(BCHG\) ein Rechteck. Folglich sind die Geraden \(HG\) und \(HC\) im Punkt \(H\) zueinander senkrecht. Da der Punkt \(T\) auf der Geraden \(HG\) liegt, ist der Abstand des Punktes \(T\) von der Geraden \(HC\) gleich der Länge der Strecke \([HT]\).
\[\left. \begin{align*} HG \perp HC& \\ T \in HC& \end{align*} \right\} \enspace \Rightarrow \enspace d\,(T;HC) = \overline{HT}\]
\[\begin{align*} d\,(T;HC) &= \overline{HT} \\[0.8em] &= \vert \overrightarrow{HT} \vert \\[0.8em] &=\vert \overrightarrow{T} - \overrightarrow{H} \vert \\[0.8em] &= \left| \begin{pmatrix} 4 \\ 8 \\ 8 \end{pmatrix} - \begin{pmatrix} 4 \\ 10 \\ 8 \end{pmatrix} \right| \\[0.8em] &= \left| \begin{pmatrix} 0 \\ -2 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^2 + (-2)^2 + 0^2} \\[0.8em] &= \sqrt{4} = 2 \end{align*}\]