Teilaufgabe 1a

Stochastik 1

    Im Rahmen der sogenannten JIM-Studie wurde in Deutschland im Jahr 2012 der Umgang von Jugendlichen im Alter von 12 bis 19 Jahren mit Informationen und Medien untersucht. In der folgenden Tabelle werden ausgewählte Ergebnisse der Studie anhand einer repräsentativen Auswahl von 200 Jugendlichen wiedergegeben, von denen 102 Jungen sind. Dabei werden für vier Geräteklassen jeweils die Anzahl der Mädchen und die Anzahl der Jungen unter den 200 ausgewählten Jugendlichen angegeben, die ein entsprechendes Gerät besitzen.

    Tabelle zur Aufgabengruppe Stochastik 1

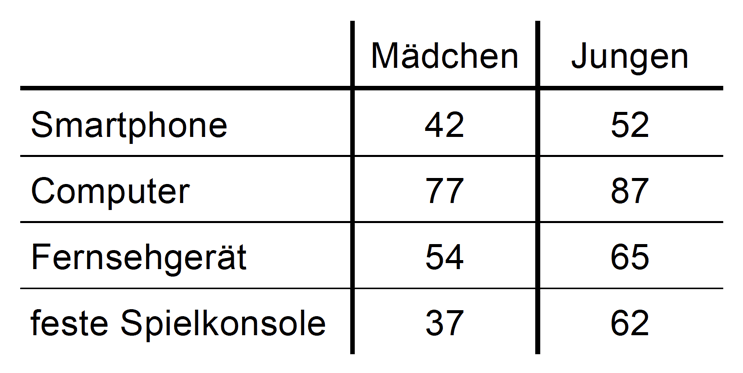
    Bestimmen Sie die Wahrscheinlichkeit dafür, dass eine aus den 200 Jugendlichen zufällig ausgewählte Person weiblich ist und kein Fernsehgerät besitzt.

    (2 BE)

    Lösung zu Teilaufgabe 1a

     

    Ereignisse:

    • \(M\,\colon\) „Eine aus 200 Jugendlichen ausgewählte Person ist ein Mädchen."
    • \(J\,\colon\) „Eine aus 200 Jugendlichen ausgewählte Person ist ein Junge."
    • \(F\,\colon\) „Eine aus 200 Jugendlichen ausgewählte Person besitzt ein Fernsehgerät."

     

    Wahrscheinlichkeit dafür, dass eine aus den 200 Jugendlichen zufällig ausgewählte Person weiblich ist und kein Fernsehgerät besitzt, formulieren:

    Es gibt 200 gleichwahrscheinliche Möglichkeiten, aus den 200 Jugendlichen zufällig eine Person auszuwählen. Die Auswahl kann also als Laplace-Experiment betrachtet werden (vgl. ABITUR SKRIPT 3.1.3 Laplace-Experiment, Laplace-Wahrscheinlichkeit).

    \[P(M \cap \overline{F}) = \frac{\vert M \cap \overline{F} \vert}{\vert \Omega\vert}\]

     

    Anzahl der Mädchen, die kein Fernsehgerät besitzen berechnen:

    Die Angabe bzw. die Tabelle informiert über die Anzahl der Mädchen, die ein Fernsehgerät besitzen und die Anzahl der Jungen.

    \[\vert M \cap F \vert = 54\]

    \[\vert J \vert = 102 \]

    \[\vert \Omega \vert = 200\]

     

    \[\begin{align*} \vert M \cap F \vert + \vert M \cap \overline{F} \vert &= \vert M \vert & &| - \vert M \cap F \vert \\[0.8em] \vert M \cap \overline{F} \vert &= \vert M \vert - \vert M \cap F \vert & &| \; \vert M \vert = \vert \Omega \vert - \vert J \vert \\[0.8em] \ &= \vert \Omega \vert - \vert J \vert - \vert M \cap F \vert \\[0.8em] &= 200 - 102 - 54 \\[0.8em] &= 44 \end{align*}\]

     

    Wahrscheinlichkeit \(P(M \cap \overline{F})\) berechnen:

     

    \[P(M \cap \overline{F}) = \frac{\vert M \cap \overline{F} \vert}{\vert \Omega\vert} = \frac{44}{200} = 0{,}22 = 22\,\%\]

    Tags
    Weitere Lösungen dieser Aufgabengruppe: Teilaufgabe 1b »