Mathematik Abitur Bayern 2015 A Analysis 1 - Aufgaben mit Lösungen

Gegeben ist die Funktion \(f \colon x \mapsto \left(x^3 - 8 \right) \cdot (2 + \ln x)\) mit maximalem Definitionsbereich D.

Geben Sie D an.

(1 BE)

Bestimmen Sie die Nullstellen von \(f\).

(2 BE)

Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f\), \(g\) und \(h\) mit \(f(x) = x^2 - x + 1\), \(g(x) = x^3 - x + 1\) und \(h(x) = x^4 + x^2 + 1\).

Abbildung 1 zeigt den Graphen einer der drei Funktionen. Geben Sie an, um welche Funktion es sich handelt. Begründen Sie, dass der Graph die anderen beiden Funktionen nicht darstellt.

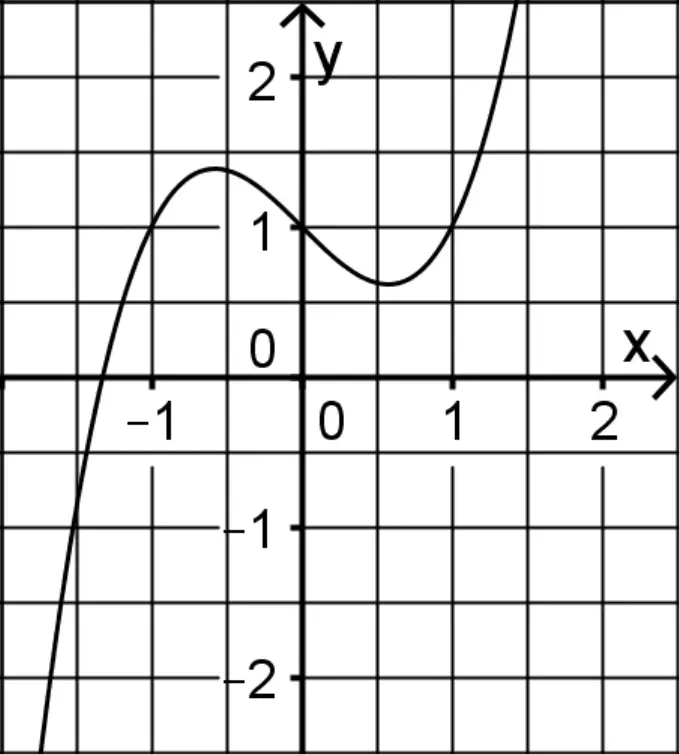Abb. 1

(3 BE)

Die erste Ableitung von \(h\) ist \(h'\).

Bestimmen Sie den Wert von \(\displaystyle \int _{0}^{1}h'(x)\,dx\). 

(2 BE)

Geben Sie einen positiven Wert für den Parameter \(a\) an, sodass die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto \sin(ax)\) eine Nullstelle in \(\displaystyle x = \frac{\pi}{6}\) hat.

(1 BE)

Ermitteln Sie den Wert des Parameters \(b\), sodass die Funktion \(g \colon x \mapsto \sqrt{x^2 - b}\) den maximalen Definitionsbereich \(\mathbb R \,\backslash\; ]-2;2[\) besitzt.

(2 BE)

Erläutern Sie, dass die in \(\mathbb R\) definierte Funktion \(h \colon x \mapsto 4 - e^x\) den Wertebereich \(]-\infty;4[\) besitzt.

(2 BE)

Abbildung 2 zeigt den Graphen einer in \(\mathbb R\) definierten differenziebaren Funktion \(g \colon x \mapsto g(x)\). Mithilfe des Newton-Verfahrens soll ein Näherungswert für die Nullstelle \(a\) von \(g\) ermittelt werden. Begründen Sie, dass weder die \(x\)-Koordinate des Hochpunkts \(H\) noch die \(x\)-Koordinate des Tiefpunkts \(T\) als Startwert des Newton-Verfahrens gewählt werden kann.

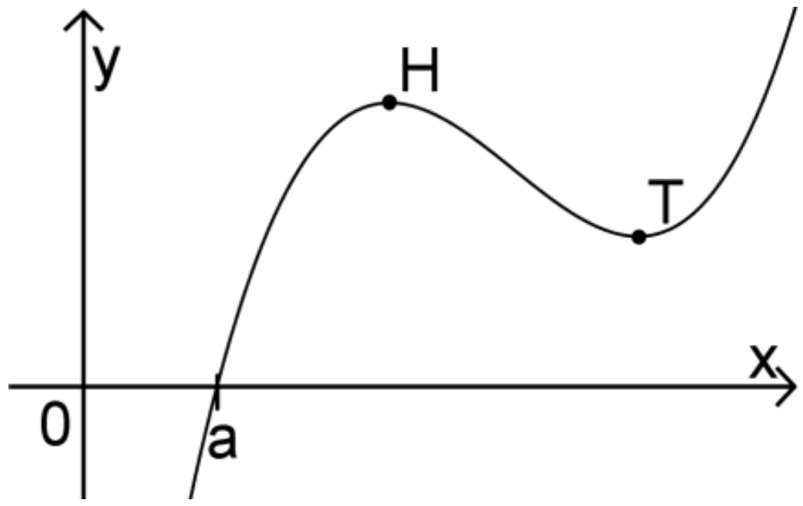Abb. 2

(2 BE)

Gegeben ist die Funktion \(f\) mit \(f(x) = x^3 - 6x^2 + 11x - 6\) und \(x \in \mathbb R\).

Weisen Sie nach, dass der Wendepunkt des Graphen von \(f\) auf der Geraden mit der Gleichung \(y = x - 2\) liegt.

(3 BE)

Der Graph von \(f\) wird verschoben. Der Punkt \((2|0)\) des Graphen der Funktion \(f\) besitzt nach der Verschiebung die Koordinaten \((3|2)\). Der verschobene Graph gehört zu einer Funktion \(h\). Geben Sie eine Gleichung von \(h\) an.

(2 BE)