Teilaufgabe 3c
Lösung zu Teilaufgabe 3c
Wertebereich einer Funktion
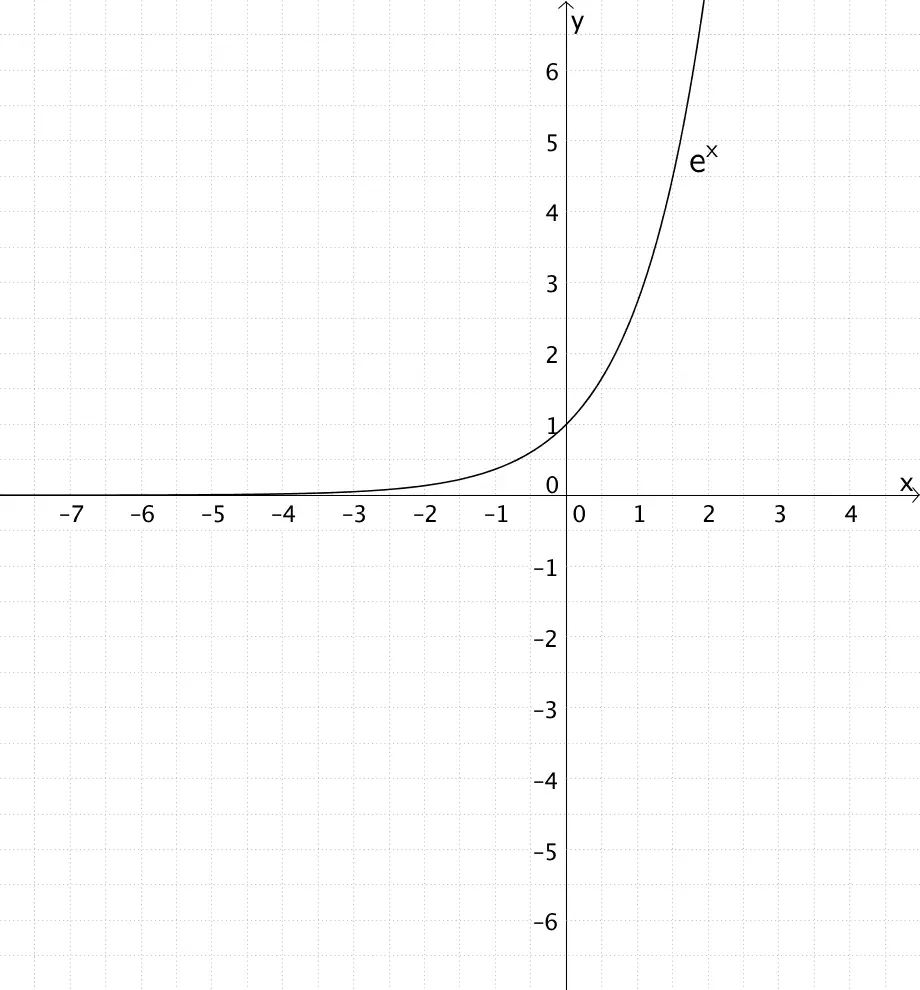
\[h(x) = 4 - e^{x}\,; \enspace D = \mathbb R\,; \enspace W = \; ]-\infty;4[\]
Der Graph \(G_{h}\) der Funktion \(h\) entsteht aus dem Graphen der Funktion \(x \mapsto e^{x}\) mit dem Wertebereich \(\mathbb R^{+}\) durch
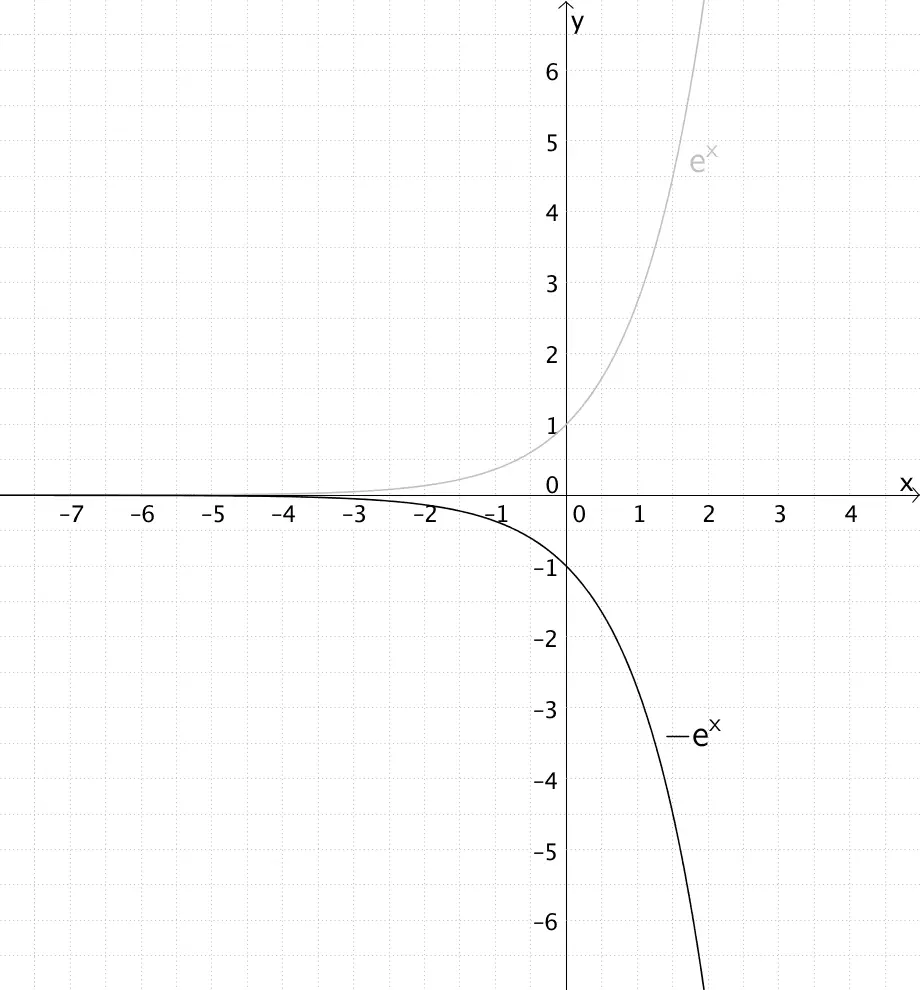
1) Spiegelung an der \(x\)-Achse
\[\Longrightarrow \quad x \mapsto - e^{x}\,; \enspace W = \mathbb R^{-} = \; ]-\infty;0[\]
und
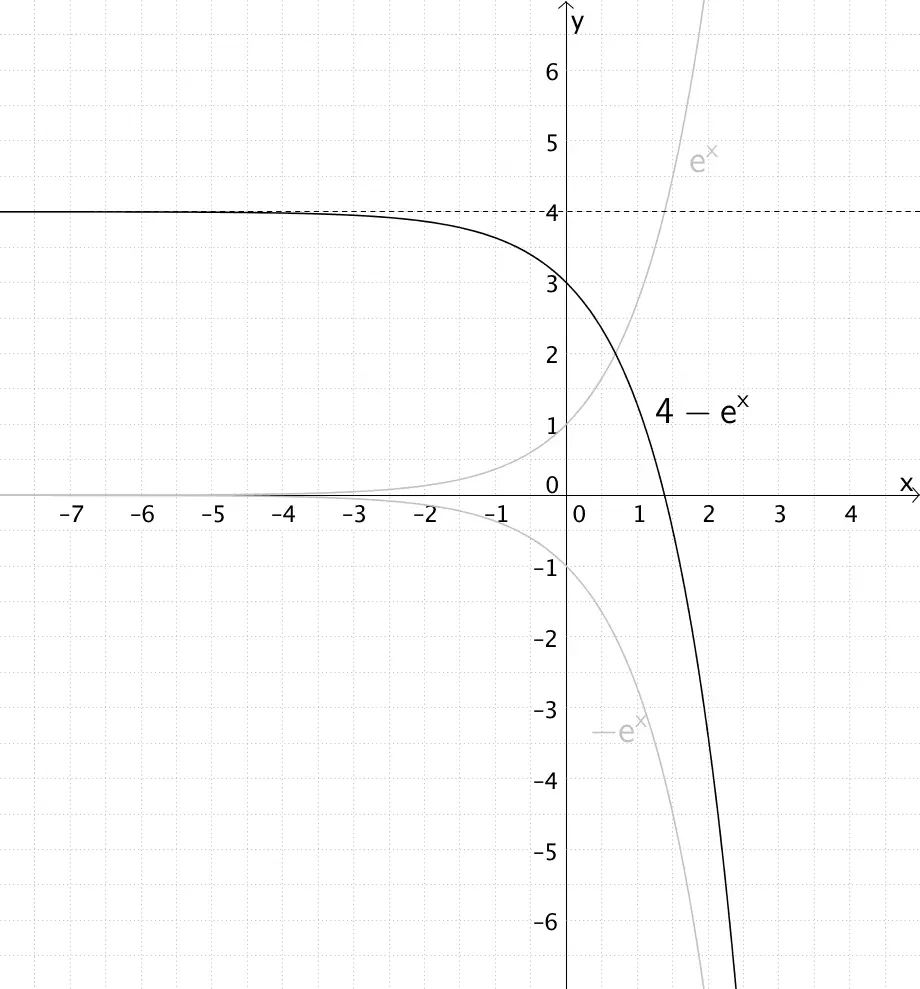
2) Verschiebung um 4 in \(y\)-Richtung.
\[\Longrightarrow \quad x \mapsto 4 - e^{x}\,; \enspace W = \; ]-\infty;4[\]
Entstehung von \(G_{h}\) aus dem Graphen der Funktion \(x \mapsto e^x\)
-
Verlauf des Graphen der Funktion \(x \mapsto e^{x}\) mit \(W = \mathbb R^{+}\)
Verlauf des Graphen der Funktion \(x \mapsto e^{x}\) mit \(W = \mathbb R^{+}\)
-
Verlauf des Graphen der Funktion \(x \mapsto -e^{x}\) mit \(W = \mathbb R^{-} = ]-\infty;0[\)
Verlauf des Graphen der Funktion \(x \mapsto -e^{x}\) mit \(W = \mathbb R^{-} = ]-\infty;0[\)
-
Verlauf des Graphen der Funktion \(h \colon x \mapsto 4 - e^{x}\) mit \(W = ]-\infty;4[\)
Verlauf des Graphen der Funktion \(h \colon x \mapsto 4 - e^{x}\) mit \(W = ]-\infty;4[\)
