Teilaufgabe 1a

Lösung zu Teilaufgabe 1a

Binomialverteilung, Wahrscheinlichkeitsrechnung

Wahrscheinlichkeit für das Ereignis \(A\) in Abhängigkeit von \(p\)

\(A\): „Der Biathlet trifft bei genau vier Schüssen."

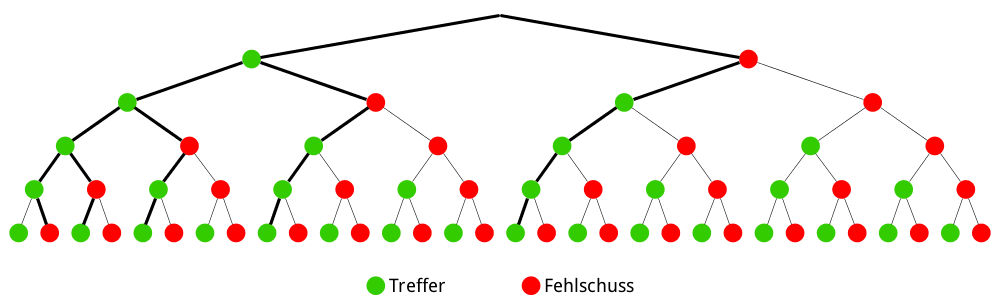
Baumdiagramm für das Ereignis \(A\): „Der Biathlet trifft bei genau vier Schüssen."

Das Ereignis \(A\) legt keine Reihenfolge für die vier Treffer fest. Bei einer Trefferwahrscheinlichkeit \(p\) beträgt die Wahrscheinlichkeit für vier Treffer \(p^{4}\) und die Wahrscheinlichkeit für einen Fehlschuss \(1 - p\).

Es gibt mehrere Möglichkeiten, wie die vier Treffer und der eine Fehlschuss auf die Abfolge der insgesamt fünf Schüsse, die der Biathlet abgibt, verteilt sein können. Die Anzahl der Möglichkeiten beschreibt der Binomialkoeffizient \(\displaystyle \binom{5}{4} = 5\) (siehe Nebenrechnung und Anmerkung unten).

Das Ereignis \(A\) setzt sich also aus fünf Ergebnissen zusammen. Die Wahrscheinlichkeit für ein Ergebnis des Ereignisses \(A\) beträgt jeweils \(p^{4} \cdot (1 - p)\).  

\[\begin{align*}P(A) &= \binom{5}{4} \cdot p^{4} \cdot (1 - p) \\[0.8em] &= 5 \cdot p^{4} \cdot (1 - p) \end{align*}\]

Nebenrechnung:

\[\begin{align*}\binom{5}{4} &= \frac{5!}{4! \cdot (5 - 4)!} \\[0.8em] &= \frac{5 \cancel{\cdot 4 \cdot 3 \cdot 2 \cdot 1}}{\cancel{4 \cdot 3 \cdot 2 \cdot 1} \cdot 1} \\[0.8em]  &= 5 \end{align*}\]

Allgemein gilt:

\[\begin{align*}\binom{n}{k = n - 1} &= \frac{n!}{k! \cdot (n - k)!} \\[0.8em] &= \frac{n!}{(n - 1)! \cdot [n - (n - 1)]!} \\[0.8em] &= \frac{n!}{(n - 1)!} \\[0.8em] &= \frac{n \cdot \cancel{(n - 1)!}}{\cancel{(n - 1)!}} \\[0.8em] &= n\end{align*}\]

\[\Longrightarrow \quad \binom{5}{4} = 5\]

Anmerkung: Die Aufgabenstellung verlangt nach einem Term, der die Wahrscheinlichkeit des Ereignisses \(A\) in Abhängigkeit von \(p\) beschreibt. Es ist nicht zwingend notwendig, den Wert des Binomialkoeffizienten zu bestimmen. Da er in diesem Fall hilfsmittelfrei einfach zu berechnen ist, sei er der Vollständigkeit halber aufgeführt.

Als Alternative kann die Wahrscheinlichkeitsverteilung einer Zufallsgröße \(X\) betrachtet werden, welche die Anzahl der Treffer beschreibt. Die Zufallsgröße \(X\) ist nach \(B(5;p)\) binomialverteilt.

Die Wahrscheinlichkeit dafür, dass die Zufallsgröße \(X\) einen bestimmten Wert annimmt, lässt sich mithilfe der Formel von Bernoulli beschreiben.

\[\begin{align*}P(A) &= P_{p}^{5}(X = 4) \\[0.8em] &= B(5;p;4) \\[0.8em] &= \binom{5}{4} \cdot p^{4} \cdot (1 - p)^{5 - 4} \\[0.8em] &= \binom{5}{4} \cdot p^{4} \cdot (1 - p) \\[0.8em] &= 5 \cdot p^{4} \cdot (1 - p)\end{align*}\]

Wahrscheinlichkeit für das Ereignis \(B\) in Abhängigkeit von \(p\)

\(B\): „Der Biathlet trifft nur bei den ersten beiden Schüssen."

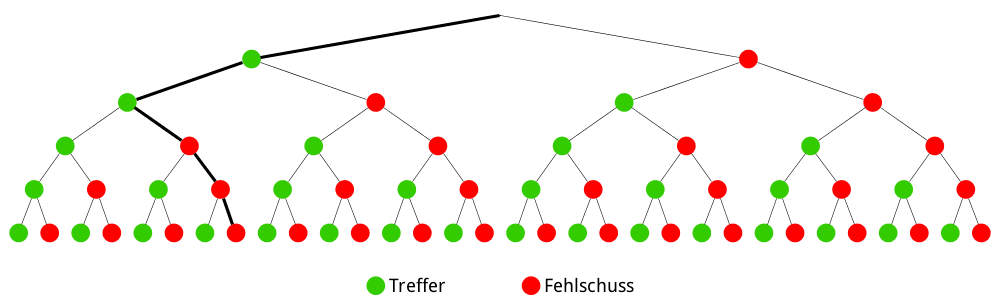
Baumdiagramm für das Ereignis \(B\): „Der Biathlet trifft nur bei den ersten beiden Schüssen."

Im Unterschied zum Ereignis \(A\) legt das Ereignis \(B\) eine ganz bestimmte Reihenfolge der Treffer und der Fehlschüsse fest. Bei einer Trefferwahrscheinlichkeit \(p\) beträgt die Wahrscheinlichkeit für die ersten beiden Treffer \(p^{2}\) und die Wahrscheinlichkeit für die drei darauf folgenden Fehlschüsse \((1 - p)^{3}\).

\[P(B) = p^{2} \cdot (1 - p)^{3}\]