Stochastik 2

In einer Urne befinden sich vier rote und sechs blaue Kugeln. Aus dieser wird achtmal eine Kugel zufällig gezogen, die Farbe notiert und die Kugel anschließend wieder zurückgelegt.

Geben Sie einen Term an, mit dem die Wahrscheinlichkeit des Ereignisses „Es werden gleich viele rote und blaue Kugeln gezogen." berechnet werden kann. 

(2 BE)

Beschreiben Sie im Sachzusammenhang jeweils ein Ereignis, dessen Wahrscheinlichkeit durch den angegebenen Term berechnet werden kann.

α) \(\displaystyle 1 - \left( \frac{3}{5} \right)^{8}\)

β) \(\displaystyle \left( \frac{3}{5} \right)^{8} + 8 \cdot \frac{2}{5} \cdot \left( \frac{3}{5} \right)^{7}\)

(3 BE)

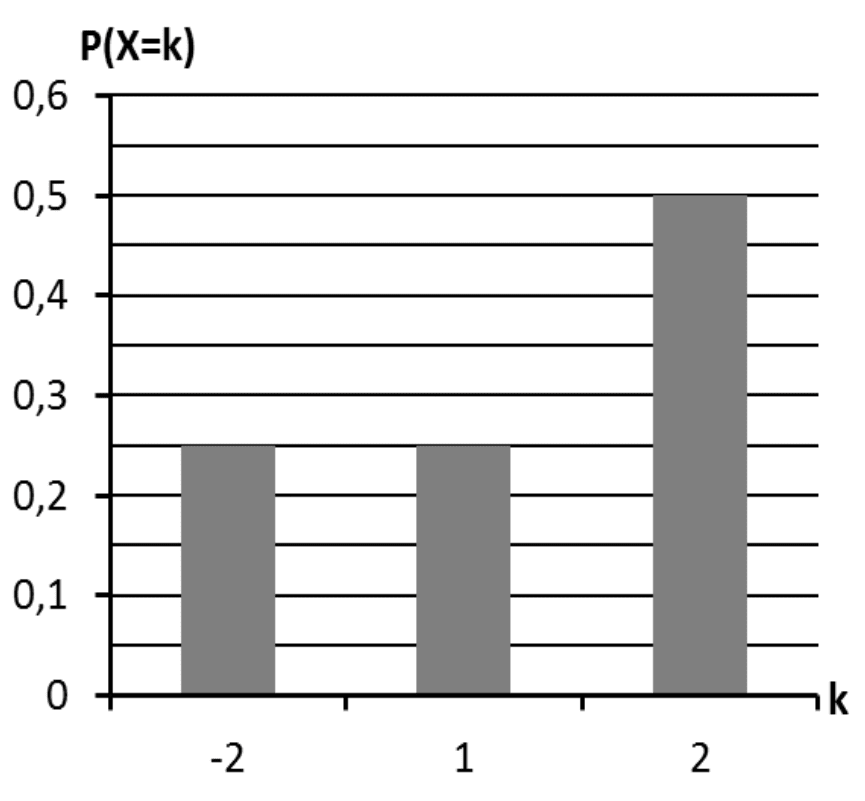
Für ein Zufallsexperiment wird eine Zufallsgröße \(X\) festgelegt, welche die drei Werte -2, 1 und 2 annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von \(X\) dargestellt.

Ermitteln Sie mithilfe der Abbildung den Erwartungswert der Zufallsgröße \(X\).

(2 BE)

Das Zufallsexperiment wird zweimal durchgeführt. Dabei wird jeweils der Wert der Zufallsgröße \(X\) notiert. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Summe dieser beiden Werte negativ ist. 

(3 BE)