Eine der Filialen der Handelskette befindet sich in einem Einkaufszentrum, das zu Werbezwecken die Erstellung einer Smartphone-App in Auftrag geben will. Diese App soll die Kunden beim Betreten des Einkaufszentrums über aktuelle Angebote und Rabattaktionen der beteiligten Geschäfte informieren. Da dies mit Kosten verbunden ist, will der Finanzchef der Handelskette einer Beteiligung an der App nur zustimmen, wenn mindestens 15 % der Kunden der Filiale bereit sind, diese App zu nutzen. Der Marketingchef warnt jedoch davor, auf eine Beteiligung an der App zu verzichten, da dies zu einem Imageverlust führen könnte.
Um zu einer Entscheidung zu gelangen, will die Geschäftsführung der Handelskette eine der beiden folgenden Nullhypothesen auf der Basis einer Befragung von 200 Kunden auf einem Signifikanzniveau von 10 % testen:
I „Weniger als 15 % der Kunden sind bereit, die App zu nutzen."
II „Mindestens 15 % der Kunden sind bereit, die App zu nutzen."
Nach Abwägung der möglichen Folgen, die der Finanzchef und der Marketingchef aufgezeigt haben, wählt die Geschäftsleitung für den Test die Nullhypothese II. Bestimmen Sie die zugehörige Entscheidungsregel.
(4 BE)
Lösung zu Teilaufgabe 2a
Signifikanztest
Zufallsgröße \(X\): „Anzahl der Kunden, die bereit sind, die App zu nutzen."
{zen-thumb-tack}Vorbemerkung:{/zen-thumb-tack}
Ein Signifikanztest für eine unbekannte Wahrscheinlichkeit ist ein Hypothesentest, welcher der Wahrscheinlichkeit für den Fehler 1. Art eine Obergrenze, das Signifikanzniveau, vorgibt. Im vorliegenden Fall ist unbekannt, mit welcher Wahrscheinlichkeit wie viele Kunden bereit sind, die App zu nutzen. Um die Wahrscheinlichkeit für den Fehler 1. Art: „Nullhypothese wird irrtümlich abgelehnt" formulieren zu können, muss eine Nullhypothese festgelegt werden. Die Nullhypothese konkretisiert die unbekannte Wahrscheinlichkeit, oft auf der Grundlage eines bisherigen Kenntnisstandes oder einer Vermutung. Ist die Nullhypothese bekannt, lässt sich damit auch der Annahme- und der Ablehnungsbereich der Nullhypothese allgemein vorformulieren. Die Durchführung des Signifikantests liefert schließlich die konkreten Grenzen, die den Annahmebereich vom Ablehnungsbereich trennen.
Analyse der Angabe:
„... auf der Basis einer Befragung von 200 Kunden ..."
\[n = 200\]
„... auf einem Signifikanzniveau von 10 % testen: ..."
\[\alpha = 0{,}10\]
„... wählt die Geschäftsleitung für den Test die Nullhypothese II."
\[\Longrightarrow \quad H_{0}\colon p \geq 0{,}15\]
Anmerkung:
Die Wahl der Nullhypothese ist keine Frage der Mathematik, sondern vielmehr eine Frage der jeweiligen Interessensperspektive. Häufig gilt es zu entscheiden, ob ein möglicher finanzieller Verlust oder ein möglicher Imageverlust schwerer wiegt (siehe Angabe). Die Wahl der Nullhypothese verfolgt die Absicht, einen sachbezogenen folgenschweren Fehler zu minimieren, indem dieser als Fehler 1. Art beschrieben wird. Die Wahrscheinlichkeit für den Fehler darf das vorgegebene Signivikanzniveau nicht überschreiten (siehe auch Teilaufgabe 2b).
Linksseitiger Signifikanztest
Einseitiger Signifikanztest zum Signifikanzniveau \(\boldsymbol{\alpha}\)
Ein einseitiger Signifikanztest zum Signifikanzniveau \(\alpha\) überprüft eine Vermutung, dass eine Wahrscheinlichkeit \(p\) größer bzw. kleiner als eine bestimmte Wahrscheinlichkeit \(p_{0}\) ist. Dabei darf die Wahrscheinlichkeit für den Fehler 1. Art höchstens den Wert des Signifikanzniveaus \(\alpha\) erreichen.
Linksseitiger Signifikanztest
\[H_0 \colon p_0 \geq p \quad H_1 \colon p_1 < p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{0; 1; ...; k\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\leq \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
Rechtsseitiger Signifikanztest
\[H_0 \colon p_0 \leq p \quad H_1 \colon p_1 > p\]
Ablehnungsbereich von \(H_0\):
\[\overline{A} = \{k + 1; ...; n\}\]
Bedingung für den Fehler 1. Art:
\[\begin{align*} P_{p_{0}}^{n}(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \in \overline{A}) &\leq \alpha \\[0.8em] P_{p_{0}}^{n}(X \geq k +1) &\leq \alpha \\[0.8em] 1 - P_{p_{0}}^{n}(X \leq k) &\leq \alpha & &| - 1 \\[0.8em] - P_{p_{0}}^{n}(X \leq k) &\leq \alpha - 1 &&| \textcolor{red}{\cdot (-1)} \\[0.8em] P_{p_{0}}^{n}(X \leq k) &\textcolor{red}{\geq} 1 - \alpha \\[1.6em] \overset{\text{ST}}{\Longrightarrow} \enspace k \enspace \Longrightarrow \enspace A, \overline{A} \end{align*}\]
ST: Stochastisches Tafelwerk
Anmerkung:
Bei einem linksseitigen Signifikanztest (rechtsseitigen Signifikanztest) liegt der Ablehnungsbereich der Nullhypothese links des Erwartungswertes (rechts des Erwartungswerts). Den Ablehnungsbereich erschließt man sich am besten sachlich logisch anhand der vorliegenden Nullhypothese. Insofern ist es für den Lösungsweg nicht zwingend notwendig, zwischen linksseitigem und rechtsseitigem Signifikanztest zu unterscheiden.
Nullhypothese \(H_{0}\colon p \geq 0{,}15\)
Gegenhypothese \(H_{1} \colon p < 0{,}15\)
Die Nullhypothese \(H_{0}\colon p \geq 0{,}15\) wird abgelehnt, wenn tendenziell wenige Kunden bereit sind, die App zu nutzen.
\(\Longrightarrow \quad\) Ablehnungsbereich von \(H_{0}\): \(\overline{A} = \{0; 1; ... ; k\}\)
\(\Longrightarrow \quad\) Annahmebereich von \(H_{0}\): \(A = \{k + 1; ... ; 200\}\)
Signifikanztest formulieren:
Die Wahrscheinlichkeit für den Fehler 1. Art darf höchstens das vorgegebene Signifikanzniveau \(\alpha\) erreichen.
Da die Entscheidung über die Annahme oder Ablehnung einer Nullhypothese aufgrund eines zufälligen Ergebnisses einer Stichprobe erfolgt, kann es zu Fehlentscheidungen kommen.
Fehler 1. Art und Fehler 2. Art
Fehler 1. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich abgelehnt.
Fehler 2. Art: Die Nullhypothese \(H_{0}\) wird irrtümlich angenommen bzw. nicht abgelehnt.
(vgl. Merkhilfe)
| \(H_{0}\) ist wahr | \(H_{0}\) ist falsch | |
| \(H_{0}\) wird abgelehnt | Fehler 1. Art | Richtige Entscheidung |
| \(H_{0}\) wird angenommen | Richtige Entscheidung | Fehler 2. Art |
Wahrscheinlichkeit \(\boldsymbol{\alpha'}\) für den Fehler 1. Art
\[\alpha' = P_{H_0} (X \in \overline{A}) = P^{n}_{p_0} (X \in \overline{A})\]
Wahrscheinlichkeit \(\boldsymbol{\beta'}\) für den Fehler 2. Art
\[\beta' = P_{H_{1}} (X \in A) = P^n_{p_{1}} (X \in A)\]
Wobei \(A\) der Annahmebereich und \(\overline{A}\) der Ablehnungsbereich der Nullhypothese \(H_0\) ist. \(H_{1}\) bezeichnet die Gegenhypothese.
\[\begin{align*} P(\text{„Fehler 1. Art"}) &\leq \alpha \\[0.8em] P^{n}_{p_{0}}(X \in \overline{A}) &\leq \alpha \\[0.8em] P^{200}_{0{,}15}(X \leq k) &\leq 0{,}10 \end{align*}\]
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
Stochastisches Tafelwerk (ST) verwenden:
\[P_{0{,}15}^{200}(X \leq k) = F_{0{,}15}^{200}(k) = \sum \limits_{i\,=\,0}^{k} B(200;0{,}15;i) \leq 0{,}10\]
\[\overset{\text{ST}}{\Longrightarrow} \quad k = 23 \quad \bigg( F_{0{,}15}^{200}(23) \enspace \overset{\text{ST}}{=} \enspace 0{,}09592 \bigg)\]
Entscheidungsregel formulieren:
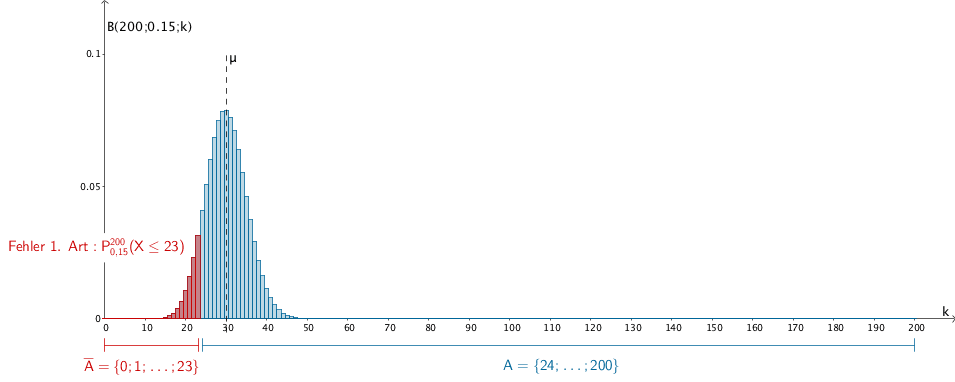
Ablehnungsbereich von \(H_{0}\): \(\overline{A} = \{0; 1; ... ; 23\}\)
Annahmebereich von \(H_{0}\): \(A = \{24; ... ; 200\}\)
Wenn mindestens 24 der 200 befragten Kunden bereit sind, die App zu nutzen, wird der Finanzchef der Handelskette einer Beteiligung an der App zustimmen.
Wahrscheinlichkeitsverteilung der nach \(B(200;0{,}15)\) binomialverteilten Zufallsgröße \(X\), Fehler 1. Art für \(k = 23\): \(P^{200}_{0{,}15}(X \leq 23) = 0{,}09592 \approx 9{,}5\,\%\)