- Details
- Kategorie: Analysis 2
Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{\ln{x}}{x^{2}}\) mit maximalem Definitionsbereich \(D\).
Geben Sie \(D\) sowie die Nullstelle von \(f\) an und bestimmen Sie \(\lim \limits_{x \, \to \, 0} f(x)\).
(3 BE)
- Details
- Kategorie: Analysis 2
Ermitteln Sie die \(x\)-Koordinate des Punkts, in dem der Graph von \(f\) eine waagrechte Tangente hat.
(4 BE)
- Details
- Kategorie: Analysis 2
Geben Sie jeweils den Term und den Definitionsbereich einer Funktion an, die die angegebene(n) Eigenschaft(en) besitzt.
Der Punkt \((2|0)\) ist ein Wendepunkt des Graphen von \(g\).
(2 BE)
- Details
- Kategorie: Analysis 2
Der Graph der Funktion \(h\) ist streng monoton fallend und rechtsgekrümmt.
(2 BE)
- Details
- Kategorie: Analysis 2
Die Abbildung zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(f\).
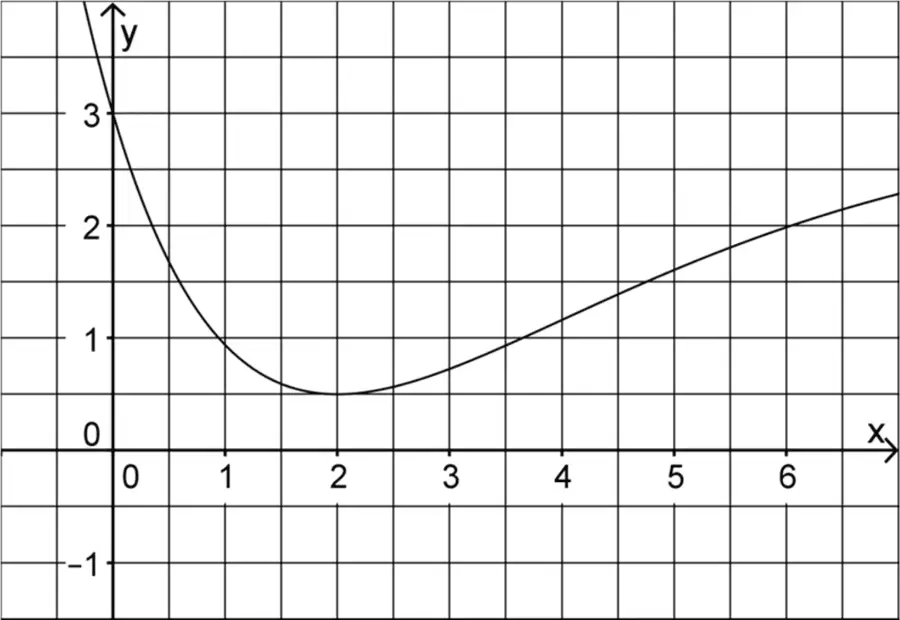
Bestimmen Sie mithilfe der Abbildung einen Näherungswert für \(\displaystyle \int_{3}^{5} f(x) \,dx\).
(2 BE)
- Details
- Kategorie: Analysis 2
Die Funktion \(F\) ist die in \(\mathbb R\) definierte Stammfunktion von \(f\) mit \(F(3) = 0\).
Geben Sie mithilfe der Abbildung einen Näherungswert für die Ableitung von \(F\) an der Stelle \(x = 2\) an.
(1 BE)
- Details
- Kategorie: Analysis 2
Zeigen Sie, dass \(\displaystyle F(b) = \int_{3}^{b} f(x) \, dx\) mit \(b \in \mathbb R\) gilt.
(2 BE)
- Details
- Kategorie: Analysis 2
Abbildung 2 zeigt den Graphen \(G_{k}\) einer in \(\mathbb R\) definierten Funktion \(k\). Skizzieren Sie in Abbildung 2 den Graphen der zugehörigen Ableitungsfunktion \(k'\). Berücksichtigen Sie dabei insbesondere einen Näherungswert für die Steigung des Graphen \(G_{k}\) an dessen Wendepunkt \((0|-3)\) sowie die Nullstelle von \(k'\).
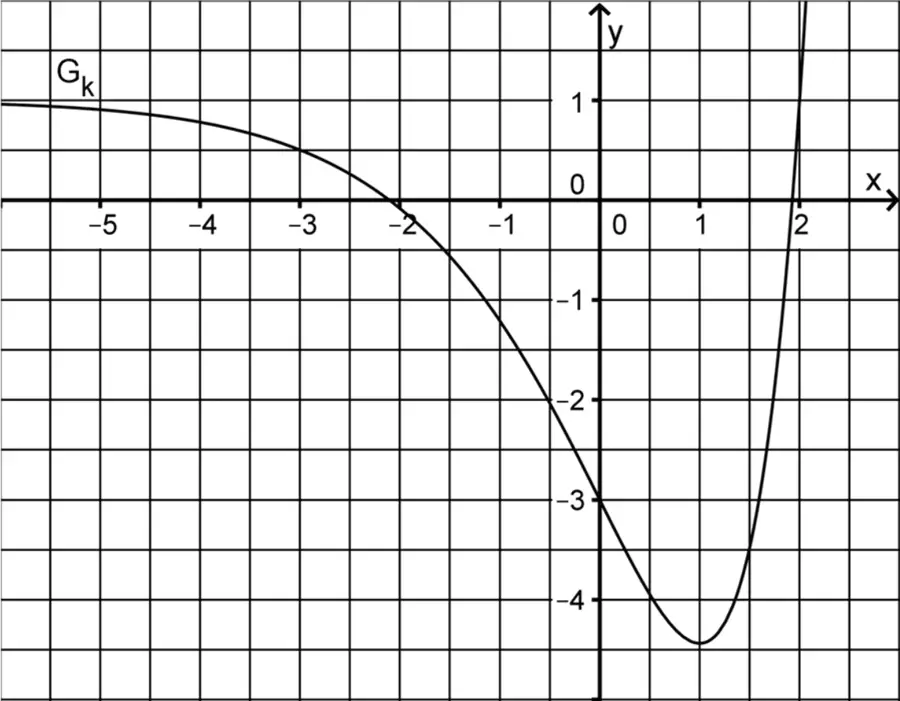
Abb. 2
(4 BE)

