Eine aus der Bevölkerung Deutschlands zufällig ausgewählte Person wird getestet; das Testergebnis ist positiv. Berechnen Sie die Wahrscheinlichkeit dafür, dass diese Person tatsächlich an einer Tierhaarallergie leidet.
(2 BE)
Lösung zu Teilaufgabe 3b
Bedingte Wahrscheinlichkeit
\(T\): „Das Testergebnis ist positiv."
\(\overline{T}\): „Das Testergebnis ist negativ."
\(A\): „Person leidet an einer Tierhaarallergie."
\(\overline{A}\): „Person leidet nicht an einer Tierhaarallergie."
Gesucht ist die bedingte Wahrscheinlichkeit \(P_{T}(A)\).
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_{T}(A) = \frac{P(A \cap T)}{P(T)}\]
Gemäß der Angabe zu Aufgabe 3 gilt:
\(P(T) = 0{,}395\), \(P_{A}(T) = 0{}85\)
Aus Teilaufgabe 3a ist bekannt:
\(P(A) = 0{,}09\)
Nach der 1. Pfadregel gilt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[P(A \cap T) = P(A) \cdot P_{A}(T)\]
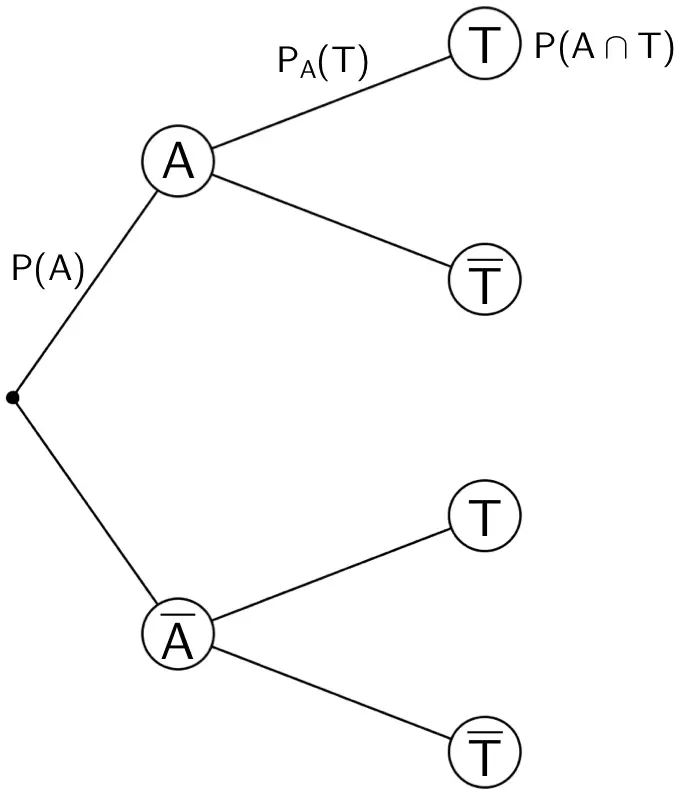
Veranschaulichung am Baumdiagramm: Berechnung der Wahrscheinlichkeit \(P(A \cap T)\) mithilfe der 1. Pfadregel
Berechnung der bedingten Wahrscheinlichkeit \(P_{T}(A)\):
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\(P(T) = 0{,}395\), \(P_{A}(T) = 0{}85\), \(P(A) = 0{,}09\)
\[\begin{align*} P_{T}(A) &= \frac{P(A \cap T)}{P(T)} & &| \; \text{1. Pfadregel anwenden} \\[0.8em] &= \frac{P(A) \cdot P_{A}(T)}{P(T)} \\[0.8em] &= \frac{0{,}09 \cdot 0{,}85}{0{,}395} \\[0.8em] &\approx 0{,}194 \\[0.8em] &=19{,}4\,\% \end{align*}\]

