Die Tangente an den Graphen von \(f\) im Punkt \(S(0|1)\) begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist.
(3 BE)
Teilaufgabe 2b
Lösung zu Teilaufgabe 2b
Gleichung einer Tangente an den Graphen einer Funktion in einem Punkt, Steigungswinkel einer Geraden, rechtwinklig gleichschenkliges Dreieck
\[f(x) = 2 \cdot e^{\frac{1}{2}x} - 1; \; D_{f} = \mathbb R\]
\[S(0|1)\]
Planskizze:
Eine Planskizze hilft, die Aufgabenstellung zu veranschaulichen. Die Skizze lässt sich mithilfe der aus Teilaufgabe 2a bekannten Nullstelle \(x = -2\ln{2} \approx -1{,}39\), dem Punkt \(S\) und in Kenntnis des charakteristischen Verlaufs des Graphen einer Natürlichen Exponentialfunktion erstellen.
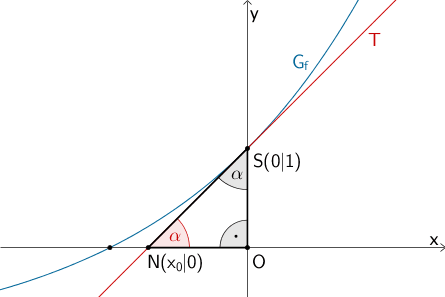
Planskizze: Graph der Funktion \(f\), Tangente \(T\) im Punkt \(S(0|1)\) und Dreieck, welches die Tangente \(T\) und die Koordinatenachsen begrenzen.
Die Tangente \(T\) schneidet die \(y\)-Achse im Punkt \(S(0|1)\) und die \(x\)-Achse im Punkt \(N(x_{0}|0)\).
Das Dreieck \(NOS\) ist rechtwinklig mit der Hypotenuse \([SN]\).
Das Dreieck \(NOS\) ist gleichschenklig,
- wenn die Katheten \([OS]\) und \([NO]\) gleich lang sind oder,
- wenn die Tangente \(T\) die \(x\)-Achse unter einem Winkel von \(\alpha = 45^{\circ}\) schneidet.
1. Lösungsansatz: Katheten gleicher Länge nachweisen
Gleichung der Tangente \(T\) an \(G_{f}\) im Punkt \(S(0|1)\) aufstellen:
Der Ansatz der Gleichung der Tangente \(T\) kann mithilfe der allgemeinen Geradengleichung oder der Tangentengleichung erfolgen.
1. Möglichkeit: Allgemeine Geradengleichung
\[T \colon y = m_{T} \cdot x + t\]
Der \(y\)-Achsenabschnitt \(t\) der Gleichung der Tangente \(T\) ist mit dem Punkt \(S(0|1) \in T\) bereits bekannt.
\[\Longrightarrow \quad T \colon y = m_{T} \cdot x + 1\]
Tangentensteigung \(m_{T}\) berechnen:
Die erste Ableitung \(f'\) an der Stelle \(x = 0\) beschreibt die Steigung \(m_{T}\) der Tangente \(T\) an den Graphen der Funktion \(f\) im Punkt \(S(0|1)\).
\[m_{T} = f'(0)\]
Erste Ableitung \(f'\) bilden:
Die erste Ableitung \(f'\) der Funktion \(f\) wird mithilfe der Ableitung der Natürlichen Exponentialfunktion, der Kettenregel sowie der Summen- und der Faktorregel formuliert.
\[f(x) = 2 \cdot e^{\frac{1}{2}x} - 1\]
\[\begin{align*} f'(x) &= 2 \cdot e^{\frac{1}{2}x} \cdot \frac{1}{2} - 0 \\[0.8em] &= e^{\frac{1}{2}x} \end{align*}\]
Tangentensteigung \(m_{T}\) berechnen:
\[m_{T} = f'(0) = e^{\frac{1}{2} \cdot 0} = e^{0} = 1\]
Damit ergibt sich die Gleichung der Tangente \(T\) zu:
\[T \colon y = x + 1\]
2. Möglichkeit: Tangentengleichung
\[T \colon y = f'(0) \cdot (x - 0) + f(0)\]
\[S(0|1) \quad \Longrightarrow \quad f(0) = 1\]
Mit \(f'(0) = 1\) (vgl. 1. Möglichkeit) folgt:
\[\begin{align*} T \colon y &= f'(0) \cdot (x - 0) + f(0) \\[0.8em] &= 1 \cdot x + 1 \\[0.8em] &= x + 1 \end{align*}\]
Nullstelle \(x_{0}\) der Tangente \(T\) berechnen:
\[T \colon y = x + 1\]
\[\begin{align*} 0 &= x + 1 & &| - 1 \\[0.8em] -1 &= x \end{align*}\]
Die Tangente \(T\) schneidet die \(x\)-Achse im Punkt \(N(-1|0)\).
Nachweis gleich langer Katheten \([OS]\) und \([NO]\) des Dreiecks \(NOS\):
\(O(0|0)\), \(S(0|1)\), \(N(-1|0)\)
\[\overline{OS} = y_{S} - y_{O} = 1 - 0 = 1\]
\[\overline{NO} = x_{O} - x_{N} = 0 - (-1) = 1\]
\[\Longrightarrow \quad \overline{OS} = \overline{NO}\]
Schlussfolgerung:
Das Dreieck, welches die Tangente an den Graphen der Funktion \(f\) im Punkt \(S\) und die Koordinatenachsen begrenzen, ist gleichschenklig.
2. Lösungsansatz: Steigungswinkel der Tangente bestimmen
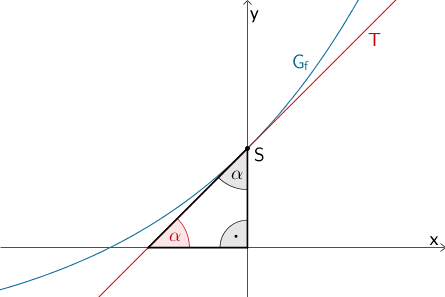
In einem gleichschenklig rechtwinkligen Dreieck schließen die Schenkel (Katheten) mit der Basis (Hypotenuse) eiinen Winkel von \(45^{\circ}\) ein. Das Dreieck, das die Tangente \(T\) und die Koordinatenachsen einschließen, ist gleichschenklig, wenn die Tangente \(T\) die \(x\)-Achse unter einem Winkel von \(45^{\circ}\) schneidet.
Im Falle einer positiven Tangentensteigung entspricht der Steigungswinkel \(\alpha\) der Tangente dem Schnittwinkel der Tangente mit der \(x\)-Achse.
\[m_{T} = \tan{\alpha}\]
\(m_{T} = 1\) (vgl. 1. Lösungsansatz)
\[\begin{align*}\tan{\alpha} &= 1 & &| \; \tan^{-1}(1) \\[2.4 em] \alpha &= 45^{\circ} \end{align*}\]
Die Tangente \(T\) schneidet die \(x\)-Achse und damit auch die \(y\)-Achse jeweils unter einem Winkel von \(45^{\circ}\).
Schlussfolgerung:
Das Dreieck, welches die Tangente an den Graphen der Funktion \(f\) im Punkt \(S\) und die Koordinatenachsen begrenzen, ist gleichschenklig.
