Die Abbildung zeigt den Graphen der in \(\mathbb R\) definierten Funktion \(g \colon x \mapsto p + q \cdot \sin\left( \frac{\pi}{r}x \right)\) mit \(p,qr \in \mathbb N\).
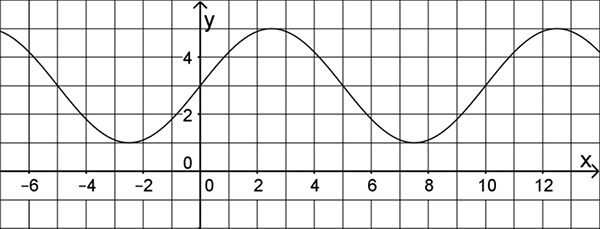
Geben Sie \(p,q\) und \(r\) an.
(3 BE)
Teilaufgabe 3a
Lösung zu Teilaufgabe 3a
Allgemeine Sinusfunktion, Streckung und Verschiebung von Funktionsgraphen
Anmerkung:
Die Parameter \(p\), \(q\) und \(r\) sind lediglich anzugeben. Jede Erklärung oder Rechnung kann entfallen.
Um die Werte der Parameter \(p\), \(q\) und \(r\) angeben zu können, wird deren Einfluss auf den Graphen der Sinusfunktion \(x \mapsto \sin{x}\) betrachtet.
Wert des Parameters \(p\)
\[g(x) = p + q \cdot \sin\left( \frac{\pi}{r}x \right); \; D_{g} = \mathbb R, \; p, q, r \in \mathbb N\]
Der Parameter \(p\) verschiebt den Graphen der Sinusfunktion \(x \mapsto \sin{x}\) in Richtung der \(y\)-Achse. Der Graph der Sinusfunktion \(x \mapsto \sin{x}\) oszilliert (schwingt) um die \(x\)-Achse \((y = 0)\). Die Abbildung zeigt, dass der Graph \(G_{g}\) der Sinusfunktion \(g\) um die Gerade mit der Gleich \(y = 3\) oszilliert. Folglich entsteht der Graph \(G_{g}\) aus dem Graphen der Sinusfunktion \(x \mapsto \sin{x}\) durch Verschiebung um drei Einheiten in Richtung der positiven \(y\)-Achse.
\[\Longrightarrow \quad p = 3\]
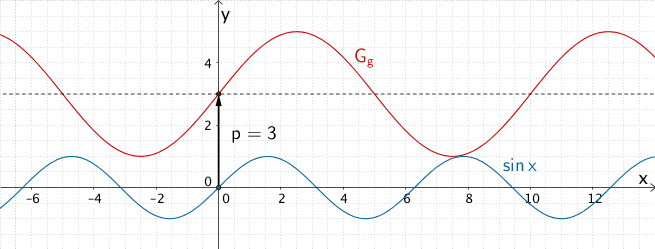
Entstehung von \(G_{g}\) durch Verschiebung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) um \(p = 3\) in Richtung der positiven \(y\)-Achse
Wert des Parameters \(q\)
\[g(x) = p + q \cdot \sin\left( \frac{\pi}{r}x \right); \; D_{g} = \mathbb R, \; p, q, r \in \mathbb N\]
Der Parameter \(q\) streckt den Graphen der Sinusfunktion \(x \mapsto \sin{x}\) in \(y\)-Richtung und entspricht der Amplitude (maximaler Ausschlag) der entstehenden Sinusfunktion \(g\). Ausgehend von der Geraden \(y = 3\), um die der Graph der Sinusfunktion \(g\) oszilliert, entnimmt man der Abbildung die Amplitude \(2\).
\[\Longrightarrow \quad q = 2\]
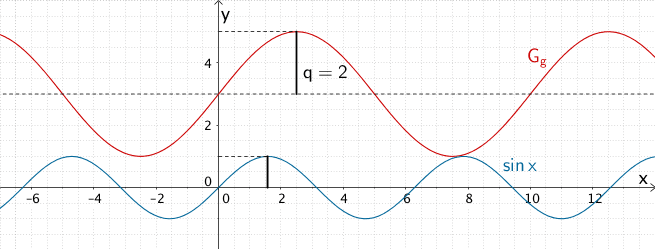
Amplitude der Sinusfunktion \(x \mapsto \sin{x}\), Amplitude der Sinusfunktion \(g\)
Der Graph der Sinusfunktion \(g\) ist gegenüber dem Graphen der Sinusfunktion \(x \mapsto \sin{x}\) mit dem Faktor \(q = 2\) in \(y\)-Richtung gestreckt.
Wert des Parameters \(r\)
\[g(x) = p + q \cdot \sin\left( \frac{\pi}{r}x \right); \; D_{g} = \mathbb R, \; p, q, r \in \mathbb N\]
Der Faktor \(\dfrac{\pi}{r}\) streckt bzw. staucht den Graphen der Sinusfunktion \(x \mapsto \sin{x}\) in \(x\)-Richtung.
Für die Periodenlänge \(p\) einer allgemeinen Sinusfunktion gilt:
\(p = \dfrac{2\pi}{b}\) (nicht zu verwechseln mit dem Parameter \(p\) der Sinusfunktion \(g\))
Dabei beschreibt \(\dfrac{1}{b}\) die Streckung bzw. \(b\) die Stauchung des Graphen der Sinusfunktion \(x \mapsto \sin{x}\) in \(x\)-Richtung.
Im Falle der vorliegenden Sinusfunktion \(g\) gilt \(b = \dfrac{\pi}{r}\).
\[\Longrightarrow \quad p = \frac{2\cancel{\pi}}{\frac{\cancel{\pi}}{r}} = 2r\]
Der Abbildung entnimmt man die Periodenlänge \(p\) der Sinusfunktion \(g\) zu : \(p = 10\).
\[\begin{align*}\Longrightarrow \quad p &= 2r \\[0.8em] 10 &= 2r & &| : 2 \\[0.8em] 5 &= r \end{align*}\]
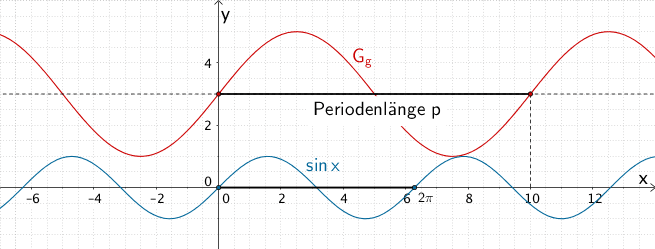
Der Graph der Sinusfunktion \(g\) ist gegenüber dem Graphen der Sinusfunktion \(x \mapsto \sin{x}\) mit dem Faktor \(\dfrac{5}{\pi} \approx 1{,}6\) in \(x\)-Richtung gestreckt.
Mit \(p = 3\), \(q = 2\) und \(r = 5\) ergibt sich der Funktionsterm der Sinusfunktion \(g\) zu:
\[g(x) = 3 + 2 \cdot \sin\left( \frac{\pi}{5}x\right) = 2 \cdot \sin\left( \frac{\pi}{5}x \right) + 3\]
