Ermitteln Sie die Koordinaten des Vektors, der sowohl ein Normalenvektor von \(E\) als auch der Ortsvektor eines Punktes der Ebene \(E\) ist.
(3 BE)
Lösung zu Teilaufgabe 2b
Lotgerade zu einer Ebene, Lotfußpunkt, lineare Abhängigkeit zweier Vektoren, Punktprobe
1. Lösungsansatz: Lotgerade durch \(O(0|0|0)\) auf die Ebene \(E\)
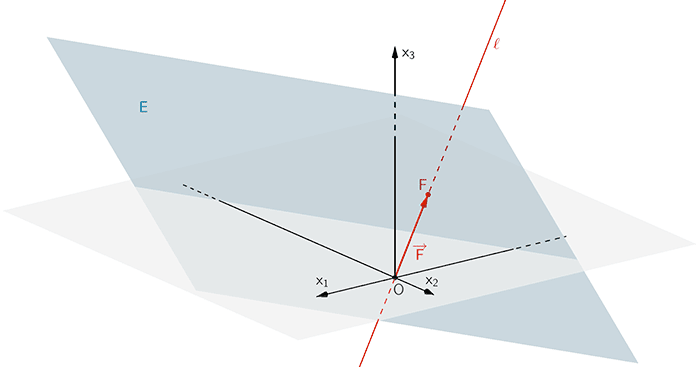
Die Lotgerade \(\ell\) zur Ebene \(E\) durch den Koordinatenursprung \(O\) schneidet die Ebene \(E\) im Lotfußpunkt \(F\) des Lotes von \(O\) auf die Ebene \(E\). Der Ortsvektor \(\overrightarrow{F}\) ist zugleich ein Normalenvektor der Ebene \(E\).
Lotgerade \(\ell\) zur Ebene \(E\) durch \(O\) formulieren:
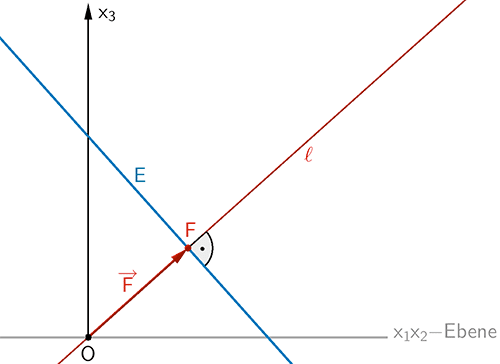
Planskizze: Lotgerade \(\ell\) zur Ebene \(E\) durch \(O\), Ortsvektor \(\overrightarrow{F}\) des Lotfußpunkts \(F\)
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\(O(0|0|0) \in \ell\), \(\ell \perp E\)
\[\ell \colon \overrightarrow{X} = \overrightarrow{O} + \mu \cdot \overrightarrow{n}_{E}; \; \mu \in \mathbb R\]
Der Normalenvektor \(\overrightarrow{n}_{E}\) ergibt sich aus der Gleichung der Ebene \(E\) in Normalenform in Koordinatendarstellung.
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon 2x_{1} + x_{2} - 2x_{3} = -18 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}\]
\[\begin{align*}\Longrightarrow \quad \ell \colon \overrightarrow{X} &= \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} \\[0.8em] &= \mu \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}; \; \mu \in \mathbb R \end{align*}\]
Koordinaten des Lotfußpunkts \(F\) berechnen:
Der Lotfußpunkt \(F\) des Lotes des Koordinatenursprungs \(O\) auf die Ebene \(E\) ist der Schnittpunkt der Lotgeraden \(\ell\) und der Ebene \(E\). Für die Berechnung der Koordinaten von \(F\) setzt man die Koordinaten des Ortsvektors \(\overrightarrow{X}\) der Geradengleichung von \(\ell\) in die Gleichung der Ebene \(E\) ein und löst die Gleichung nach dem Parameter \(\mu\) auf.
Der Wert des Parameters \(\mu\) in die Gleichung der Lotgeraden \(\ell\) eingesetzt, ergibt den Ortsvektor des Lotfußpunkts \(F\).
\[\ell \colon \overrightarrow{X} = \mu \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 2\mu \\ \mu \\ -2\mu \end{pmatrix}\]
\[E \colon 2x_{1} + x_{2} - 2x_{3} = -18\]
\[\begin{align*} \ell \cap E \colon 2 \cdot 2\mu + \mu - 2 \cdot (-2\mu) &= -18 \\[0.8em] 9\mu &= - 18 & &| : 9 \\[0.8em] \mu &= -2 \end{align*}\]
Parameterwert \(\mu = -2\) in die Gleichung der Lotgeraden \(\ell\) einsetzen:
\[F \in \ell \colon \overrightarrow{F} = (-2) \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} -4 \\ -2 \\ 4 \end{pmatrix}\]
Der Ortsvektor \(\overrightarrow{F} = \begin{pmatrix} -4 \\ -2 \\ 4 \end{pmatrix}\) des Lotfußpunkts \(F\) des Lotes des Koordinatenursprungs \(O\) auf die Ebene \(E\) ist zugleich Normalenvektor der Ebene \(E\).
2. Lösungsansatz: Lineare Abhängigkeit zweier Vektoren, Punktprobe
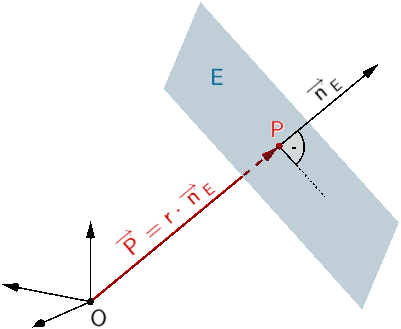
Planskizze: Der Punkt \(P\) liegt in der Ebene E \((P \in E)\). Der Ortsvektor \(\overrightarrow{P}\) ist genau dann zugleich ein Normalenvektor der Ebene \(E\), wenn sich dieser als reelles Vielfaches \(r\) eines beliebigen Normalenvektors der Ebene \(E\) beschreiben lässt. Mit anderen Worten: Der Ortsvektor \(\overrightarrow{P}\) und ein Normalenvektor \(\overrightarrow{n}_{E}\) müssen linear abhängig sein.
Lineare (Un-)Abhängigkeit von zwei Vektoren
Zwei Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) sind
linear abhängig, wenn
\(\overrightarrow{a} \parallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} = k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
linear unabhängig, wenn
\(\overrightarrow{a} \nparallel \overrightarrow{b}\quad\) bzw. \(\quad\overrightarrow{a} \neq k \cdot \overrightarrow{b}\,; \enspace k \in \mathbb R \quad\) gilt.
Lineare (Un-)Abhängigkeit von drei Vektoren
Drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) sind
linear abhängig, wenn
sie in einer Ebene liegen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) eine eindeutige Lösung hat.
linear unabhängig, wenn
sie den Raum \(\mathbb R^{3}\) aufspannen bzw. wenn
die lineare Vektorgleichung \(\overrightarrow{c} = r \cdot \overrightarrow{a} + s \cdot \overrightarrow{b}\) keine Lösung hat.
Bei der Untersuchung der linearen (Un)Abhängigkeit dreier Vektoren spielt es keine Rolle, welche der drei Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) oder \(\overrightarrow{c}\) man als Linearkombination der beiden anderen Vektoren darzustellen versucht.
\[\overrightarrow{P} = r \cdot \overrightarrow{n}_{E}; \; r \in \mathbb R\]
Ein Normalenvektor \(\overrightarrow{n}_{E}\) der Ebene \(E\) kann der gegebenen Ebenengleichung in Normalenform in Koordinatendarstellung (Koordinatenform) entnommen werden (vgl. Angabe Aufgabe 2).
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[E \colon 2x_{1} + x_{2} - 2x_{3} = -18 \quad \Longrightarrow \quad \overrightarrow{n}_{E} = \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix}\]
Es muss also gelten:
\[\overrightarrow{P} = r \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 2r \\ r \\ -2r \end{pmatrix}; \; r \in \mathbb R \quad \Longrightarrow \quad P(2r|r|-2r)\]
Punktprobe \(P \in E\):
Da der Punkt \(P\) in der Ebene \(E\) liegen soll, muss der Punkt \(P\) die Gleichung der Ebene \(E\) erfüllen. Somit lässt sich der Wert des Parameters \(r\) mithilfe einer Punktprobe berechnen. Hierfür werden die Koordinaten des Punktes \(P\) in die Gleichung der Ebene \(E\) eingesetzt und die Gleichung nach dem Parameter \(r\) aufgelöst.
\[P(2r|r|-2r)\]
\[E \colon 2x_{1} + x_{2} - 2x_{3} = -18\]
\[\begin{align*}P \in E \colon 2 \cdot 2r + r - 2 \cdot (-2r) &= -18 \\[0.8em] 9r &= -18 & &| : 9 \\[0.8em] r &= -2 \end{align*}\]
Ortsvektor \(\overrightarrow{P}\) berechnen:
\[\overrightarrow{P} = r \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} = (-2) \cdot \begin{pmatrix} 2 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} -4 \\ -2 \\ 4 \end{pmatrix}\]
Der Ortsvektor \(\overrightarrow{P} = \begin{pmatrix} -4 \\ -2 \\ 4 \end{pmatrix}\) des Punktes \(P(-4|-2|4) \in E\) ist zugleich ein Normalenvektor der Ebene \(E\).


