Zeichnen Sie den Graphen von \(F\) unter Berücksichtigung der bisherigen Ergebnisse sowie des Funktionswerts \(F(0)\) im Bereich \(-0{,}3 \leq x \leq 3{,}5\) in Abbildung 1 ein.
(4 BE)
Teilaufgabe 1e
Lösung zu Teilaufgabe 1e
Funktionsgraph zeichnen
\[F(x) = 2e^{-x} - 2e^{-2x}; \; D_{F} = \mathbb R\]
Bisherige Ergebnisse:
- \[\lim \limits_{x\,\to\,+\infty} F(x) = 0\]
- \(G_{F}\) besitzt den absoluten Hochpunkt \(HoP(\ln{2}|0{,}5)\).
- \(G_{F}\) besitzt den Wendepunkt \(W\Big(\ln{4} \Big| \frac{3}{8} \Big)\).
Funktionswert \(F(0)\)
\[F(0) = 2e^{0} - 2e^{-2 \cdot 0} = 2 \cdot 1 - 2 \cdot 1 = 0\]
\(\Longrightarrow \quad G_{F}\) verläuft durch den Koordinatenursprung.
Zeichnung des Graphen der Stammfunktion \(F\)
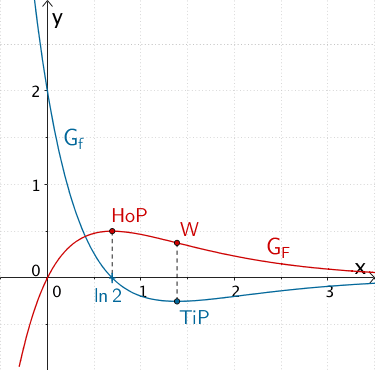
Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto 2e^{-x} \cdot \left( 2e^{-x} - 1 \right)\) und Graph der in \(\mathbb R\) definierten Stammfunktion \(F \colon x \mapsto 2e^{-x} - 2e^{-2x}\).
