Im Zelt ist eine Lichtquelle so aufgehängt, dass sie von jeder der vier Wände einen Abstand von 50 cm hat. Ermitteln Sie die Koordinaten des Punkts, der im Modell die Lichtquelle darstellt.
(4 BE)
Lösung zu Teilaufgabe d
Abstand Punkt - Ebene, Trigonometrische Beziehungen im rechtwinkligen Dreieck
1. Lösungsansatz: Abstand Punkt - Ebene
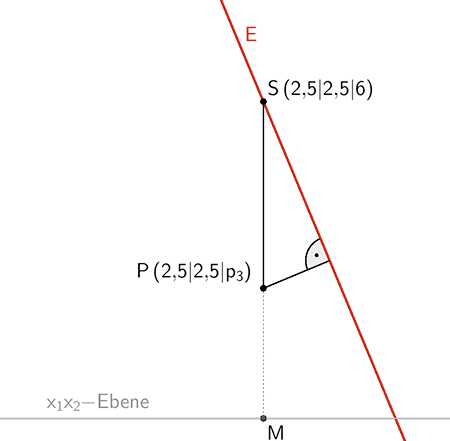
Planskizze: Den Koordinaten der Spitze \(S\) der Pyramide \(ABCDS\) ist zu entnehmen, dass der Punkt \(S\) über dem Mittelpunkt \(M\) der Diagonalen der quadratischen Grundfläche \(ABCD\) liegt (gerade Pyramide).
Damit eine Lichtquelle \(P\) von jeder der vier Zeltwände den gleichen Abstand hat, muss der Punkt \(P\) auf der Strecke \([MS]\) liegen. Die Strecke \([MS]\) ist die Höhe der Pyramide und steht senkrecht auf der \(x_{1}x_{2}\)-Ebene, in der sich die Grundfläche der Pyramide befindet.
Die Koordinaten des Punktes \(P\) lassen sich bis auf die \(x_{3}\)-Koordinate festlegen. Der Wert, den die \(x_{3}\)-Koordinate annehmen kann, ist durch die Lage der Grundfläche (\(x_{1}x_{2}\)-Ebene) und die Höhe der Pyramide eingeschränkt. Die Höhe der Pyramide beträgt 6 m (vgl. Angabe).
\(P(2{,}5|2{,}5|p_{3})\) mit \(p_{3} \in \; ]0;6[\)
Betrachtet wird beispielsweise der Abstand \(d(P;E)\) des Punktes \(P\) von der Ebene \(E\), in der das Dreieck \(CDS\) (Zeltwand) liegt (vgl. Angabe). Dieser Abstand soll 50 cm betragen. Eine Längeneinheit entspricht einem Meter (vgl. Angabe).
\[d(P;E) = 0{,}5\]
Anmerkung:
Dieser Lösungsansatz ist nur möglich, weil bereits zwei Koordinaten des Punktes \(P\) bekannt sind.
Es ist ebenso möglich, den Abstand \(d(P;F)\) des Punktes \(P\) von der Ebene \(F\) zu betrachten (vgl. Teilaufgabe b).
![Punkt P auf der Strecke [MS] im gleichen Abstand von der Ebene E und der Ebene F Punkt P auf der Strecke [MS] im gleichen Abstand von der Ebene E und der Ebene F](/images/stories/B2017_PT_B_G_2/B2017_PT_B_G_2_d_2.png)
Punkt \(P \in [MS]\) (Lichtquelle) im gleichen Abstand von der Ebene \(E\) und der Ebene \(F\)
Abstand des Punktes \(P\) von der Ebene \(E\) beschreiben:
Der Abstand des Punktes \(P\) von der Ebene \(E\) lässt sich mithilfe der Hesseschen Normalenform der Ebene \(E\) formulieren. Man erhält die Hessesche Normalenform der Gleichung der Ebene \(E\), indem man die vorliegende Gleichung der Ebene \(E\) in Normalenform durch den Betrag des Normalenvektors \(\overrightarrow{n}_{E}\) dividiert.
Abstand eines Punktes von einer Ebene
Für den Abstand \(d(P;E)\) eines Punktes \(P(p_{1}|p_{2}|p_{3})\) zu einer in der Hesseschen Normalenform (HNF) vorliegenden Ebene \(E\) gilt:
Vektordarstellung
\[E \colon \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \overrightarrow{n}^{0}_{E} \circ (\overrightarrow{P} - \overrightarrow{A}) \right|\]
Koordinatendarstellung
\[E \colon \frac{n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} = 0 \enspace (\text{HNF})\]
\[d(P;E) = \left| \frac{n_{1}p_{1} + n_{2}p_{2} + n_{3}p_{3} + n_{0}}{\sqrt{n_{1}^{2} + n_{2}^{2} + n_{3}^{2}}} \right|\]
Dabei ist \(\overrightarrow{n}^{0}_{E} = \dfrac{\overrightarrow{n}_{E}}{\vert \overrightarrow{n}_{E} \vert}\) der Einheitsvektor des Normalenvektors \(\overrightarrow{n}_{E}\) der Ebene \(E\).
Hessesche Normalenform der Ebene \(E\):
\(E \colon 12x_{2} + 5x_{3} = 60\) (vgl. Angabe)
\[E \colon 12x_{2} + 5x_{3} - 60 = 0\]
\[\overrightarrow{n}_{E} = \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix}\]
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\vert \overrightarrow{n}_{E} \vert = \left| \begin{pmatrix} 0 \\ 12 \\ 5 \end{pmatrix} \right| = \sqrt{0^{2} + {12}^{2} + 5^{2}} = \sqrt{169} = 13\]
\[\begin{align*}E_{\text{HNF}} \colon \frac{12x_{2} + 5x_{3} - 60}{\vert \overrightarrow{n}_{E} \vert} &= 0 \\[0.8em] E_{\text{HNF}} \colon \frac{12x_{2} + 5x_{3} - 60}{13} &= 0 \end{align*}\]
Damit lässt sich der Abstand \(d(P;E)\) des Punktes \(P\) von der Ebene \(E\) wie folgt beschreiben:
\(P(2{,}5|2{,}5|p_{3})\) mit \(p_{3} \in ]0;6[\)
\[\begin{align*}d(P;E) &= \left| \frac{12p_{2} + 5p_{3} - 60}{13} \right| \\[0.8em] &= \left| \frac{12 \cdot 2{,}5 + 5p_{3} - 60}{13} \right| \\[0.8em] &= \left| \frac{5p_{3} - 30}{13} \right| \end{align*}\]
Koordinate \(p_{3}\) des Punkts \(P\) berechnen:
\[\begin{align*}d(P;E) &= 0{,}5 \\[0.8em] \left| \frac{5p_{3} - 30}{13} \right| &= 0{,}5 & &| \cdot 13 \\[0.8em] \vert 5p_{3} - 30 \vert &= 6{,}5 \end{align*}\]
Die Betragsgleichung wird durch Fallunterscheidung gelöst. Für den Fall \(5p_{3} - 30 > 0\) können die Betragsstriche entfallen. Für den Fall \(5p_{3} - 30 < 0\) wird der Term \(-(5p_{3} - 30)\) betrachtet, um die Funktionsweise des Betrags zu beschreiben.
1. Fall: \(5p_{3} - 30 > 0\)
\[\begin{align*} 5p_{3} - 30 &= 6{,}5 & &| + 30 \\[0.8em] 5p_{3} &= 36{,}5 & &| : 5 \\[0.8em] p_{3} &= 7{,}3 \end{align*}\]
Dies ist nicht der gesuchte Wert, denn es gilt \(p_{3} \in \; ]0;6[\). Der Punkt \((2{,}5|2{,}5|7{,}3)\) liegt oberhalb von Punkt \(S\) auf der Geraden \(MS\) und hat den Abstand \(d = 0{,}5\) von der Ebene \(E\). Der Wert \(p_{3} = 7{,}3\) ist daher im Sachzusammenhang falsch.
2. Fall: \(5p_{3} - 30 < 0\)
\[\begin{align*} -(5p_{3} - 30) &= 6{,}5 \\[0.8em] -5p_{3} + 30 &= 6{,}5 & &| - 30 \\[0.8em] -5p_{3} &= -23{,}5 & &| : 5 \\[0.8em] p_{3} &= 4{,}7 \end{align*}\]
\[\Longrightarrow \quad P(2{,}5|2{,}5|4{,}7)\]
Damit die Lichtquelle von jeder der vier Zeltwände einen Abstand von 50 cm hat, muss diese 4,7 m über dem Mittelpunkt der Diagonalen der quadratischen Grundfläche des Zeltbodens angebracht werden.
Alternative 1: Lage des Punktes \(P\) bezüglich der Ebene \(E\) und des Koordinatenursprungs berücksichtigen.
Der Abstand eines Punktes von einer Ebene wird in der Regel als positiver Wert aufgefasst. Deshalb wird der Betrag des den Abstand beschreibenden Terms formuliert.
Darf die Abstandsbestimmung dagegen beliebige Werte in \(\mathbb R\) annehmen, informiert das Ergebnis neben dem Abstand zusätzlich über die Lage des betrachteten Punktes bezüglich der Ebene und des Koordinatenursprungs.
Bei der Bestimmung des Abstands \(d(P;E)\) eines Punktes \(P\) von einer Ebene \(E\) lassen sich folgende mögliche Ergebnisse unterscheiden:
- \(d(P;E) > 0\): Der Punkt \(P\) und der Koordinatenursprung liegen auf verschiedenen Seiten der Ebene \(E\).
- \(d(P;E) = 0\): Der Punkt \(P\) liegt in der Ebene \(E\) \((P \in E)\).
- \(d(P;E) < 0\): Der Punkt \(P\) und der Koordinatenursprung liegen auf der gleichen Seite der Ebene \(E\).
Mithilfe der Zeichnung aus Teilaufgabe a wird deutlich, dass der Punkt \(P(2{,}5|2{,}5|p_{3})\) und der Koordinatenursprung (Punkt \(A\)) auf der gleichen Seite der Ebene \(E\) (Dreieck \(CDS\)) liegen.
Es liegt also der Fall \(d(P;E) < 0\) vor.
\[\begin{align*}d(P;E) &= -0{,}5 \\[0.8em] \frac{5p_{3} - 30}{13} &= -0{,}5 & &| \cdot 13 \\[0.8em] 5p_{3} - 30 &= -6{,}5 & &| + 30 \\[0.8em] 5p_{3} &= 23{,}5 & &| : 5 \\[0.8em] p_{3} &= 4{,}7 \end{align*}\]
\[\Longrightarrow \quad P(2{,}5|2{,}5|4{,}7)\]
Alternative 2: Punkt \(P\) (Lichtquelle) allgemein durch die Gerade \(MS\) beschreiben
Der Punkt \(P\) liegt auf der Geraden \(MS\). Diese ist die Lotgerade durch die Pyramidenspitze \(S(2{,}5|2{,}5|6)\) auf die \(x_{1}x_{2}\)-Ebene.
Ein Normalenvektor der \(x_{1}x_{2}\)-Ebene ist beispielsweise \(\overrightarrow{n}_{x_{1}x_{2}} = \begin{pmatrix} 0 \\ 0 \\ 1\end{pmatrix}\).
Lotgerade auf eine Ebene
\[E\,\colon \overrightarrow{n}_E \circ (\overrightarrow{X} - \overrightarrow{A}) = 0; \quad P\,(p_1|p_2|p_3)\]
Die Lotgerade \(\ell\) mit \(P \in \ell\) auf eine Ebene \(E\) ist durch den Ortsvektor \(\overrightarrow{P}\) und den Normalenvektor \(\overrightarrow{n}_E\) eindeutig bestimmt:
\[\ell\,\colon \overrightarrow{X} = \overrightarrow{P} + \lambda \cdot \overrightarrow{n}_E; \; \lambda \in \mathbb R\]
\[MS \colon \overrightarrow{X} = \overrightarrow{S} + \mu \cdot \overrightarrow{n}_{x_{1}x_{2}}\]
\[MS \colon \overrightarrow{X} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}; \; \mu \in \mathbb R\]
\[P \in MS: \overrightarrow{P} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 + \mu \end{pmatrix} \quad \Longrightarrow \quad P(2{,}5|2{,}5|6 + \mu)\]
Abstand \(d(P;E)\) des Punktes \(P\) von der Ebene \(E\) beschreiben (vgl. oben):
\[\begin{align*}d(P;E) &= \left| \frac{12p_{2} + 5p_{3} - 60}{13} \right| \\[0.8em] &= \left| \frac{12 \cdot 2{,}5 + 5 \cdot (6 + \mu) - 60}{13} \right| \\[0.8em] &= \left| \frac{5\mu}{13} \right| \end{align*}\]
Koordinaten des Punkts \(P\) berechnen:
\[\begin{align*}d(P;E) &= 0{,}5 \\[0.8em] \left| \frac{5\mu}{13} \right| &= 0{,}5 & &| \cdot 13 \\[0.8em] \vert 5\mu \vert &= 6{,}5 & &| : 5 \\[0.8em] \vert \mu \vert &= 1{,}3 \end{align*}\]
\[\Longrightarrow \quad \mu_{1} = 1{,}3; \; \mu_{2} = -1{,}3\]
Es ergeben sich folgende zwei Punkte \(P_{1}\) und \(P_{2}\), welche auf der Geraden \(MS\) liegen und von der Ebene \(E\) den Abstand \(d(P;E) = 0{,}5\) haben.
\[\overrightarrow{P_{1}} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 + 1{,}3 \end{pmatrix} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 7{,}3 \end{pmatrix} \quad \Longrightarrow \quad P_{1}(2{,}5|2{,}5|7{,}3)\]
\[\overrightarrow{P_{2}} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 6 - 1{,}3 \end{pmatrix} = \begin{pmatrix} 2{,}5 \\ 2{,}5 \\ 4{,}7 \end{pmatrix} \quad \Longrightarrow \quad P_{1}(2{,}5|2{,}5|4{,}7)\]
Der Punkt \(P(2{,}5|2{,}5|4{,}7)\) liegt mit \(p_{3} \in\; ]0;6[\) auf der Strecke \([MS]\) und ist daher der im Sachzusammenhang richtige Punkt, der im Modell die Lichtquelle darstellt.
2. Lösungsansatz: Trigonometrische Beziehungen im rechtwinkligen Dreieck
![Der Mittelpunkt M der Diagonalen der quadratischen Grundfläche, der Mittelpunkt der Strecke [CD] und der Punkt S bilden ein rechtwinkliges Dreieck. Der Mittelpunkt M der Diagonalen der quadratischen Grundfläche, der Mittelpunkt der Strecke [CD] und der Punkt S bilden ein rechtwinkliges Dreieck.](/images/stories/B2017_PT_B_G_2/B2017_PT_B_G_2_d_3.png)
Planskizze: Der Mittelpunkt \(M\) der Diagonalen der quadratischen Grundfläche \(ABCD\), der Mittelpunkt \(M_{[CD]}\) der Strecke \([CD]\) und die Spitze \(S\) der Pyramide \(ABCDS\) bilden das rechtwinklige Dreieck \(MM_{[CD]}S\).
Die Strecke \([M_{[CD]}S]\) ist die Höhe des Dreiecks \(CDS\), das in der Ebene \(E\) liegt. Der Abstand \(d\) des Punktes \(P\) (Lichtquelle) von der Strecke \([M_{[CD]}S]\) entspricht dem Abstand der Lichtquelle von der Zeltwand, die durch das Dreieck \(CDS\) dargestellt wird.
Die Strecken \([MS]\) und \([M_{[CD]}S]\) schließen den Winkel \(\varepsilon\) ein.
Der Punkt \(P(2{,}5|2{,}5|p_{3})\) liegt auf der Strecke \([MS]\), welche die Höhe der geraden Pyramide \(ABCDS\) ist (vgl. 1. Lösungsansatz).
![Pyramide ABCDS, Ebene E, rechtwinkliges Dreieck, das der Mittelpunkt M der Diagonalen der quadratischen Grundfläche, der Mittelpunkt der Strecke [CD] und die Spitze S bilden. Pyramide ABCDS, Ebene E, rechtwinkliges Dreieck, das der Mittelpunkt M der Diagonalen der quadratischen Grundfläche, der Mittelpunkt der Strecke [CD] und die Spitze S bilden.](/images/stories/B2017_PT_B_G_2/B2017_PT_B_G_2_d_4.png)
Pyramide \(ABCDS\), Ebene \(E\) und rechtwinkliges Dreieck \(MM_{[CD]}S\)
Es gelten die folgenden trigonometrischen Beziehungen:
Trigonometrische Beziehungen im rechtwinkligen Dreieck (vgl. Merkhilfe)
\[\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}\]
\[\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}\]
\[\tan \alpha = \frac{\text{Gegenkathete}}{\text{Ankathete}}\]
\[\begin{align*}\tan{\varepsilon} &= \frac{\overline{MM_{[CD]}}}{\overline{MS}} & &| \; \overline{MM_{[CD]}} = \frac{1}{2} \cdot \overline{BC} = 2{,}5 \\[0.8em] &= \frac{2{,}5}{6} \\[0.8em] &= \frac{5}{12} & &| \; \text{TR:} \; \tan^{-1}(\dots) \\[3.2em] \varepsilon &\approx 22{,}62^{\circ} \end{align*}\]
\(d = 0{,}5\) (Eine Längeneinheit entspricht einem Meter, vgl. Angabe)
\[\begin{align*}\sin{\varepsilon} &= \frac{d}{\overline{PS}} \\[0.8em] \Longleftrightarrow \enspace \overline{PS} &= \frac{d}{\sin{\varepsilon}} \\[0.8em] &= \frac{0{,}5}{\sin{22{,}62^{\circ}}} \\[0.8em] &\approx 1{,}3 \end{align*}\]
Koordinate \(p_{3}\) des Punktes \(P\) berechnen:
\[\overline{MP} = \overline{MS} - \overline{PS} = 6 - 1{,}3 = 4{,}7\]
\[\Longrightarrow \quad P(2{,}5|2{,}5|4{,}7)\]
Damit die Lichtquelle von jeder der vier Zeltwände einen Abstand von 50 cm hat, muss diese 4,7 m über dem Mittelpunkt der Diagonalen der quadratischen Grundfläche des Zeltbodens angebracht werden.

