Das abgebildete Baumdiagramm stellt ein zweistufiges Zufallsexperiment mit den Ereignissen \(A\) und \(B\) sowie deren Gegenereignissen \(\overline{A}\) und \(\overline{B}\) dar.
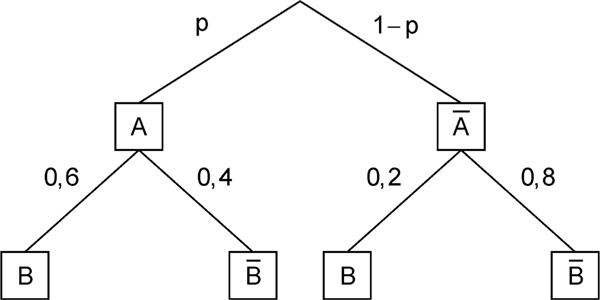
Bestimmen Sie den Wert von \(p\) so, dass das Ereignis \(B\) bei diesem Zufallsexperiment mit der Wahrscheinlichkeit \(0,3\) eintritt.
(2 BE)
Lösung zu Teilaufgabe 2a
Nach der ersten und zweiten Pfadregel gilt:
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
\[\begin{align*}P(B) &= 0{,}3 \\[0.8em] \underbrace{\underbrace{0{,}6 \cdot p}_{\large{\text{1. Pfadregel}}} + \enspace \underbrace{0{,}2 \cdot (1 - p)}_{\large{\text{1. Pfadregel}}}}_{\large{\text{2. Pfadregel}}} &= 0{,}3 \\[0.8em] 0{,}6p + 0{,}2 - 0{,}2p &= 0{,}3 \\[0.8em] 0{,}4p + 0{,}2 &= 0{,}3 &&| -0{,}2 \\[0.8em] 0{,}4p &= 0{,}1 &&| : 0{,}4 \\[0.8em] p &= 0{,}25 \end{align*}\]


