- Details
- Kategorie: Analysis 1
Gegeben ist die in \(\mathbb R^{+}\) definierte Funktion \(f \colon x \mapsto 2 \cdot \left( \left( \ln{x} \right)^{2} - 1\right)\). Abbildung 1 zeigt den Graphen \(G_{f}\) von \(f\).
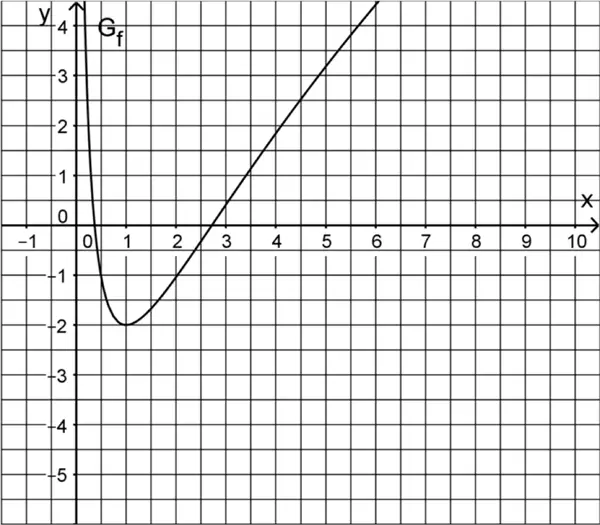 Abb. 1
Abb. 1
Zeigen Sie, dass \(x = e^{-1}\) und \(x = e\) die einzigen Nullstellen von \(f\) sind, und berechnen Sie die Koordinaten des Tiefpunkts \(T\) von \(G_{f}\).
(zur Kontrolle: \(f'(x) = \frac{4}{x} \cdot \ln{x}\))
(5 BE)
- Details
- Kategorie: Analysis 1
Zeigen Sie, dass \(G_{f}\) genau einen Wendepunkt \(W\) besitzt, und bestimmen Sie dessen Koordinaten sowie die Gleichung der Tangente an \(G_{f}\) im Punkt \(W\).
(zur Kontrolle: \(x\)-Koordinate von \(W\): \(e\))
(6 BE)
- Details
- Kategorie: Analysis 1
Begründen Sie, dass \(\lim \limits_{x\,\to\,0}f'(x) = -\infty\) und \(\lim \limits_{x\,\to\,+\infty}f'(x) = 0\) gilt. Geben Sie \(f'(0{,}5)\) und \(f'(10)\) auf eine Dezimale genau an und zeichnen Sie den Graphen der Ableitungsfunktion \(f'\) unter Berücksichtigung aller bisherigen Ergebnisse in Abbildung 1 ein.
(6 BE)
- Details
- Kategorie: Analysis 1
Begründen Sie unter Zuhilfenahme von Abbildung 1, dass es zwei Werte \(c \in \; ]0;6[\) gibt, für die gilt: \(\displaystyle \int_{e^{-1}}^{c} f(x) dx = 0\).
(3 BE)
- Details
- Kategorie: Analysis 1
Die gebrochen-rationale Funktion \(h \colon x \mapsto 1{,}5x - 4{,}5 + \frac{1}{x}\) mit \(x \in \mathbb R \backslash \{0\}\) stellt in einem gewissen Bereich eine gute Näherung für \(f\) dar.
Geben Sie die Gleichungen der beiden Asymptoten des Graphen von \(h\) an.
(2 BE)
- Details
- Kategorie: Analysis 1
Im IV. Quadranten schließt \(G_{f}\) zusammen mit der \(x\)-Achse und den Geraden mit den Gleichungen \(x = 1\) und \(x = 2\) ein Flächenstück ein, dessen Inhalt etwa \(1{,}623\) beträgt. Ermitteln Sie die prozentuale Abweichung von diesem Wert, wenn bei der Berechnung des Flächeninhalts die Funktion \(h\) als Näherung für die Funktion \(f\) verwendet wird.
(5 BE)
- Details
- Kategorie: Analysis 1
Durch Spiegelung von \(G_{f}\) an der Geraden \(x = 4\) entsteht der Graph einer in \(]-\infty;8[\) definierten Funktion \(g\). Dieser Graph wird mit \(G_{g}\) bezeichnet.
Zeichnen Sie \(G_{g}\) in Abbildung 1 ein.
(2 BE)
- Details
- Kategorie: Analysis 1
Die beschriebene Spiegelung von \(G_{f}\) an der Geraden \(x = 4\) kann durch eine Spiegelung von \(G_{f}\) an der \(y\)-Achse mit anschließender Verschiebung ersetzt werden. Beschreiben Sie diese Verschiebung und geben Sie \(a, b \in \mathbb R\) an, sodass \(g(x) = f(ax + b)\) für \(x \in \; ]-\infty;8[\) gilt.
(3 BE)
- Details
- Kategorie: Analysis 1
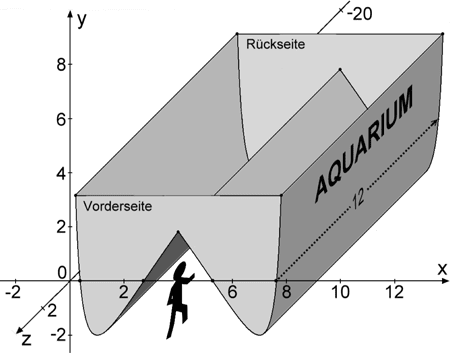 Abb. 2
Abb. 2
Im Folgenden wird die „w-förmige" Kurve \(k\) betrachtet, die sich aus dem auf \(0{,}2 \leq x \leq 4\) beschränkten Teil von \(G_{f}\) und dem auf \(4 < x \leq 7{,}8\) beschränkten Teil von \(G_{g}\) zusammensetzt. Die Kurze \(k\) wird um 12 Einheiten in negative \(z\)-Richtung verschoben. Die dabei überstrichene Fläche dient als Modell für ein 12 Meter langes Aquarium, das durch zwei ebene Wände an Vorder- und Rückseite zu einem Becken ergänzt wird (vgl. Abbildung 2). Dabei entspricht eine Längeneinheit im Koordinatensystem einem Meter in der Realität.
Die Aquariumwände bilden an der Unterseite einen Tunnel, durch den die Besucher hindurchgehen können. Berechnen Sie die Größe des Winkels, den die linke und die rechte Tunnelwand miteinander einschließen.
(3 BE)
- Details
- Kategorie: Analysis 1
Das Aquarium wird vollständig mit Wasser gefüllt.
Berechnen Sie die größtmögliche Wassertiefe des Aquariums.
(2 BE)
- Details
- Kategorie: Analysis 1
Das Volumen des Wassers im Aquarium lässt sich analog zum Rauminhalt eines Prismas mit Grundfläche \(G\) und Höhe \(h\) berechnen. Erläutern Sie, dass der Term \(\displaystyle 24 \cdot \int_{0{,}2}^{4} \left( f(0{,}2) - f(x) \right) dx\) das Wasservolumen im vollgefüllten Aquarium in Kubikmetern beschreibt.
(3 BE)

