Begründen Sie, dass \(F_{1}\) höchstens vier Nullstellen hat.
(2 BE)
Lösung zu Teilaufgabe 1f
Nach dem Hauptsatz der Differential- und Integralrechnung ist die Integralfunktion \(F_{1}\) eine Stammfunktion von \(f\),
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Die Funktion \(f\) ist eine ganzrationalen Funktion dritten Grades (vgl. Angabe). Jede Stammfunktion von \(f\) und somit auch die Integralfunktion \(F_{1}\), ist dann eine ganzrationale Funktion vierten Grades, welche höchstens vier Nullstellen haben kann.
Alternative Begründung:
Aus der Angabe zu den Teilaufgaben 1d und 1e ist bekannt, dass die Integralfunktion \(\displaystyle F_{1} \colon x \mapsto \int_{1}^{x}f(t)dt\) drei positive Nullstellen hat.
Mithilfe von Abb. 1 kann genau eine weitere vierte negative Nullstelle begründet werden.
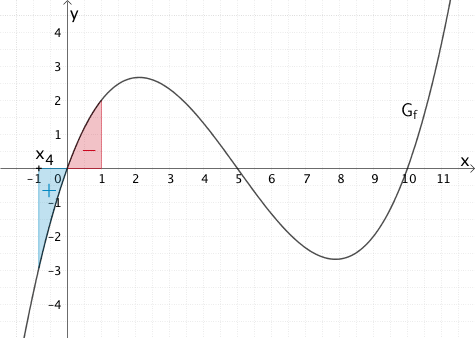
\(G_{f}\) verläuft im Intervall \(]0;1]\) oberhalb der \(x\)-Achse und im Intervall \(]-\infty;0[\) unterhalb der \(x\)-Achse. Folglich gibt es eine vierte negative Nullstelle \(x_{4} < 0\), sodass die Flächenbilanz von \(F_{1}(x_{4}) = \displaystyle \int_{1}^{x_{4}}f(t)dt\) gleich Null ist.
Eine weitere negative Nullstelle von \(F_{1}\) kann es nicht geben, da \(G_{f}\) für \(x < x_{4}\) fortwährend unterhalb der \(x\)-Achse verläuft und der Flächenzuwachs somit stets positiv ist. Analog dazu kann es keine weitere positive Nullstelle als die aus den Lösungen zu Teilaufgaben 1d und 1e bekannten positiven Nullstellen \(x_{1}\), \(x_{2}\) und \(x_{3}\) von \(F_{1}\) geben, da \(G_{f}\) für \(x > x_{3}\) (vgl. Teilaufgabe 1e) stets oberhalb der \(x\)-Achse verläuft.
{zen-hand-o-right}Anmerkungen{/zen-hand-o-right}
Für \(x < 1\) ist die obere Integrationsgrenze der Integralfunktion \(\displaystyle F_{1} \colon x \mapsto \int_{1}^{x}f(t)dt\) kleiner als die feste untere Integrationsgrenze. Deshalb gehen Flächenstücke oberhalb der \(x\)-Achse negativ und Flächenstücke unterhalb der \(x\)-Achse positiv in die Flächenbilanz ein.
Die alternative Begründung ist nicht nur deutlich zeitaufwendiger, sie setzt auch die Lösungen der Teilaufgaben 1d und 1e voraus.


