Teilaufgabe c

Lösung zu Teilaufgabe c

 

Ein Trapez ist ein Viereck mit zwei parallelen Seiten. Sonderformen eines Trapezes sind: Parallelogramm, Raute, Rechteck und Quadrat.

 

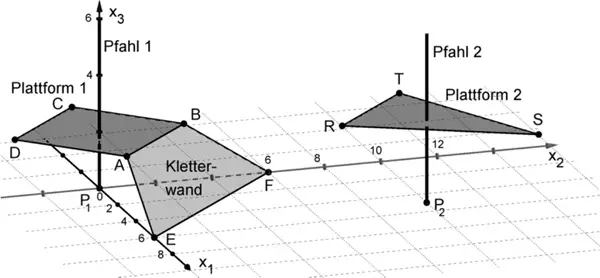
Die Abbildung lässt vermuten, dass die Strecken \([AB]\) und \([EF]\) zueinander parallel sind. Dies ist dann der Fall, wenn die Verbindungsvektoren \(\overrightarrow{AB}\) und \(\overrightarrow{EF}\) linear abhängig sind, d.h. ein Vielfaches voneinander sind, wenn also beispielsweise \(\overrightarrow{AB} = k \cdot \overrightarrow{EF}\) mit \(k \in \mathbb R\) gilt.

 

\(\overrightarrow{AB} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix}\) (vgl. Teilaufgabe a)

 

Verbindungsvektor \(\overrightarrow{EF}\) berechnen:

 

\(E(6|0|0)\), \(F(0|6|0)\)

 

\[\overrightarrow{EF} = \overrightarrow{F} - \overrightarrow{E} = \begin{pmatrix} 0 \\ 6 \\ 0 \end{pmatrix} - \begin{pmatrix} 6 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} -6 \\ 6 \\ 0 \end{pmatrix}\]

 

Prüfen, ob die Vektoren \(\overrightarrow{AB}\) und \(\overrightarrow{EF}\) linear abhängig sind:

\[\begin{align*}\begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix} = \frac{1}{2} \cdot \begin{pmatrix} -6 \\ 6 \\ 0 \end{pmatrix} \quad &\Longrightarrow \quad \overrightarrow{AB} = \frac{1}{2} \cdot \overrightarrow{EF} \\[0.8em] &\Longrightarrow \quad \overrightarrow{AB} \parallel \overrightarrow{EF} \\[0.8em] &\Longrightarrow \quad [AB] \parallel [EF] \end{align*}\]

 

Also hat die Kletterwand die Form eines Trapezes.