Ein Glücksrad besteht aus fünf gleich großen Sektoren. Einer der Sektoren ist mit „0" beschriftet, einer mit „1" und einer mit „2"; die beiden anderen Sektoren sind mit „9" beschriftet.
Das Glücksrad wird viermal gedreht. Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zahlen 2, 0, 1 und 9 in der angegebenen erzielt werden.
(2 BE)
Lösung zu Teilaufgabe 1a
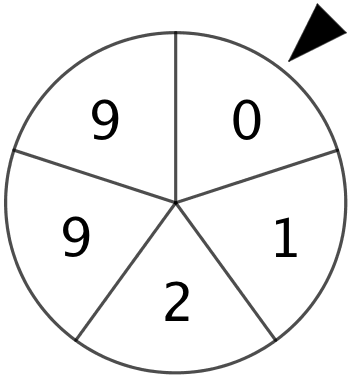
Glücksrad mit beispielhafter Beschriftung der fünf gleich großen Sektoren.
\[P(\{0\}) = \frac{1}{5}; \; P(\{1\}) = \frac{1}{5}; \; P(\{2\}) = \frac{1}{5}; P(\{9\}) = \frac{2}{5}\]
\[\begin{align*}P(\{2, 0, 1, 9\}) &= P(\{2\}) \cdot P({0}) \cdot P(\{1\}) \cdot P(\{9\}) \\[0.8em] &= \frac{1}{5} \cdot \frac{1}{5} \cdot \frac{1}{5} \cdot \frac{2}{5} \\[0.8em] &= \frac{2}{625} \end{align*}\]

