Teilaufgabe 1b

Lösung zu Teilaufgabe 1b

 

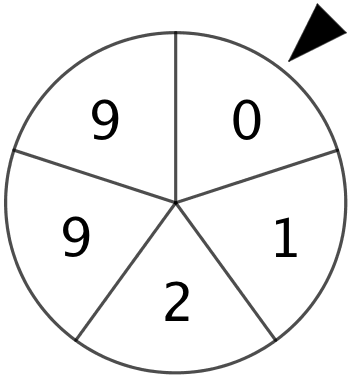
Glücksrad mit beispielhafter Beschriftung der fünf gleich großen Sektoren.

 

\[P(\{0\}) = \frac{1}{5}; \; P(\{1\}) = \frac{1}{5}; \; P(\{2\}) = \frac{1}{5}; P(\{9\}) = \frac{2}{5}\]

 

Das Ereignis „Die Summe der erzielten Zahlen ist mindestens 11" enthält die Ergebnisse \(\{2, 9\}\), \(\{9, 2\}\) und \(\{9, 9\}\).

Die Wahrscheinlichkeit des Ereignisses „Die Summe der erzielten Zahlen ist mindestens 11" ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu dem Ereignis gehören.

 

\[\begin{align*}P(\text{„Summe ist mind. 11"}) &= P(\{2, 9\}) + P(\{9, 2\}) + P(\{9, 9\}) \\[0.8em] &= \frac{1}{5} \cdot \frac{2}{5} + \frac{2}{5} \cdot \frac{1}{5} + \frac{2}{5} \cdot \frac{2}{5} \\[0.8em]&=  \frac{2}{25} + \frac{2}{25} + \frac{4}{25} \\[0.8em] &= \frac{8}{25} \end{align*}\]

 

Veranschaulichung mithilfe eines Baumdiagramms:

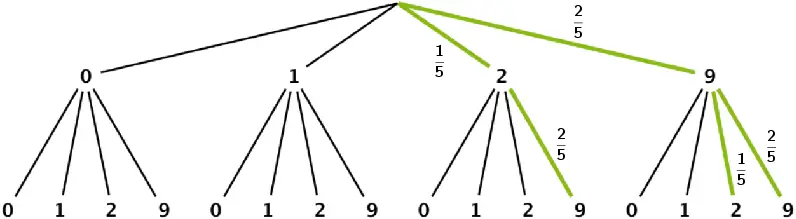
Relevante Pfade des Ereignisses „Die Summe der erzielten Zahlen ist mindestens 11"

 

Mithilfe der 1. und 2. Pfadregel gilt:

\[\begin{align*}P(\text{„Summe ist mind. 11"}) &= P(\{2, 9\}) + P(\{9, 2\}) + P(\{9, 9\}) \\[0.8em] &= \underbrace{\underbrace{\frac{1}{5} \cdot \frac{2}{5}}_{\text{1. Pfadregel}} + \underbrace{\frac{2}{5} \cdot \frac{1}{5}}_{\text{1. Pfadregel}} +  \underbrace{\frac{2}{5} \cdot \frac{2}{5}}_{\text{1. Pfadregel}}}_{\text{2. Pfadregel}} \\[0.8em]&=  \frac{2}{25} + \frac{2}{25} + \frac{4}{25} \\[0.8em] &= \frac{8}{25} \end{align*}\]