Das Baumdiagramm in Abbildung 2 gehört zu einem Zufallsexperiment mit den stochastisch unabhängigen Ereignissen \(A\) und \(B\). Bestimmen Sie die Wahrscheinlichkeit des Ereignisses \(B\).
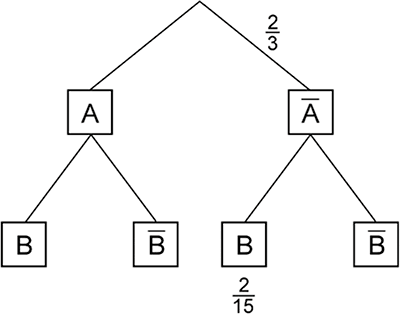Abb. 2
(3 BE)
Teilaufgabe 3
Abb. 2Lösung zu Teilaufgabe 3
Nach der zweiten Pfadregel gilt:
\[P(B) = P(A \cap B) + P(\overline{A} \cap B)\]
Nach der Verzweigungsregel (Knotenregel) gilt:
\[\textcolor{#0087c1}{P(A)} = 1 - P(\overline{A}) = 1 - \frac{2}{3} = \textcolor{#0087c1}{\frac{1}{3}}\]
Wegen der stochastischen Unabhängigkeit der Ereignisse \(A\) und \(B\) treten an den Pfaden der zweiten Stufe des Baumdiagramms in Abbildung 2 die gleichen Wahrscheinlichkeiten auf.
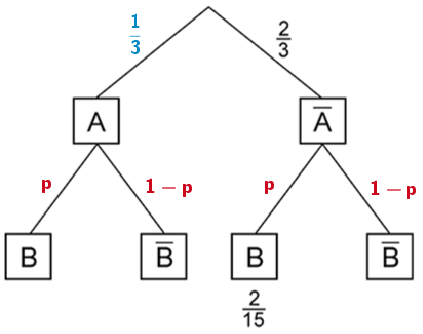
Mithilfe der ersten Pfadregel folgt:
\[\begin{align*}\frac{2}{3} \cdot \textcolor{#cc071e}{p} &= \frac{2}{15} &&| \cdot \frac{3}{2} \\[0.8em] \textcolor{#cc071e}{p} &= \frac{\cancel{2}}{15} \cdot \frac{3}{\cancel{2}} \\[0.8em] &= \textcolor{#cc071e}{\frac{1}{5}}\end{align*}\]
Somit ergibt sich:
\[\begin{align*}P(B) &= P(A \cap B) + P(\overline{A} \cap B) \\[0.8em] &= \textcolor{#0087c1}{\frac{1}{3}} \cdot \textcolor{#cc071e}{\frac{1}{5}} + \frac{2}{15} \\[0.8em] &= \frac{1}{15} + \frac{2}{15} \\[0.8em] &= \frac{3}{15} \\[0.8em] &= \frac{1}{5} \end{align*}\]
