Berechnen Sie auf der Grundlage des Modells die Größe des Winkels \(\alpha\), den das Plateau und die Fahrbahn an der Kante zur Abfahrt einschließen (vgl. Abbildung 2).
(2 BE)
Lösung zu Teilaufgabe 2d
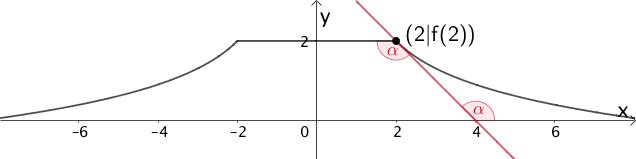
Die Größe des Winkels \(\alpha\) entspricht der Größe des Steigungswinkels der Tangente an den Graphen der Funktion \(f\) (Profillinie der Abfahrt) im Punkt \((2|f(2))\) (Wechselwinkel, Z-Winkel).
Für den Steigungswinkel \(\alpha\) der Tangente mit der Steigung \(m\) gilt:
Steigungswinkel \(\alpha\) einer Gerade \(g \colon y = m \cdot x +t\)
\[\tan \alpha = m \qquad \alpha \neq 90^\circ\]
\[m = \tan{\alpha}\]
Für die Tangentensteigung \(m\) gilt:
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
\[m = f'(2)\]
Mit \(f'(x) = \dfrac{1}{1 - x}\) (vgl. Teilaufgabe 2b) folgt somit:
\[\begin{align*} \tan{\alpha} &= f'(2) \\[0.8em] \tan{\alpha} &= \frac{1}{1 - 2} \\[0.8em] \tan{\alpha} &= -1 &&| \; \text{TR:} \; \tan^{-1}(-1) \\[0.8em] \alpha &= -45^{\circ} &&| + 180^{\circ} \; \text{(positiver Winkel gegen UZS)} \\[0.8em] \alpha &= 135^{\circ} \end{align*}\]

