Gegeben ist die Funktion \(f \colon x \mapsto \dfrac{4x}{(x + 1)^{2}}\) mit Definitionsmenge \(D_{f} = \mathbb R \backslash \{-1\}\). Die Abbildung zeigt den Verlauf des Graphen \(G_{f}\) von \(f\) im I. Quadranten.
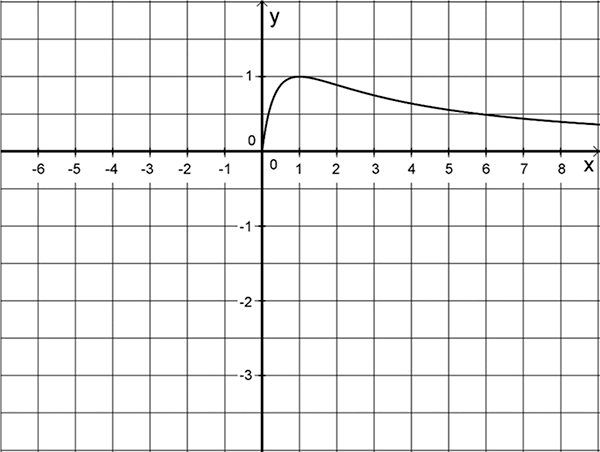
Begründen Sie, dass \(x = 0\) die einzige Nullstelle von \(f\) ist. Geben Sie die Gleichung der senkrechten Asymptote von \(G_{f}\) an und begründen Sie anhand des Funktionsterms von \(f\), dass \(G_{f}\) die Gerade mit der Gleichung \(y = 0\) als waagrechte Asymptote besitzt.
(3 BE)
Lösung zu Teilaufgabe a
\[f(x) = \frac{4x}{(x + 1)^{2}}; \; D_{f} = \mathbb R \backslash \{-1\}\]
Begründung, dass \(x = 0\) die einzige Nullstelle von \(f\) ist
Die Nullstelle der gebrochenrationalen Funktion \(f\) ist die Nullstelle des Zählers \(4x\), die nicht zugleich Nullstelle des Nenners sein darf.
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
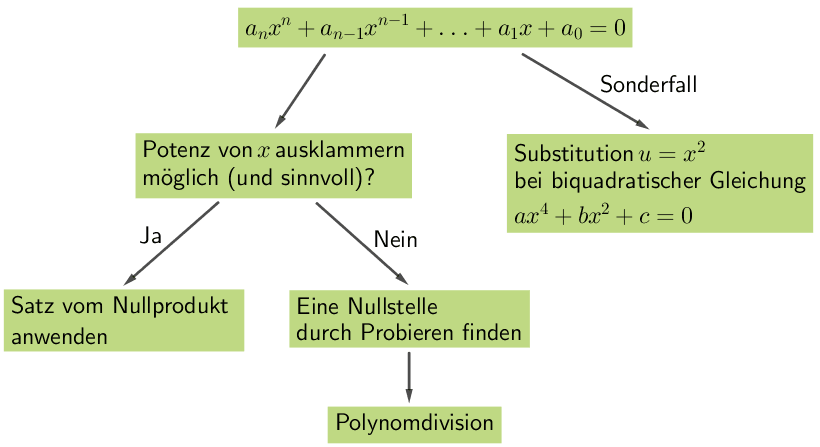
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
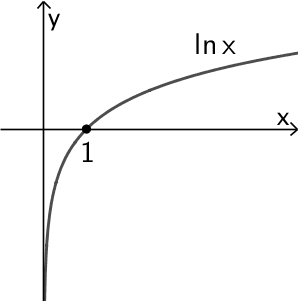
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[f(x) = 0 \quad \Longrightarrow \quad 4x = 0 \quad \Longleftrightarrow \quad x = 0\]
Somit ist \(x = 0\) die einzige Nullstelle von \(f\), da diese nicht zugleich Nullstelle des Nenners ist.
Anmerkung:
Ist \(x_0\) eine Nullstelle der Zählerfunktion \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle der Nennerfunktion \(\boldsymbol{n(x)}\), so besitzt eine gebrochnrationale Funktion \(f \colon x \mapsto \dfrac{z(x)}{n(x)}\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Gleichung der senkrechten Asymptote von \(G_{f}\)
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
Senkrechte Asymptote mit der Gleichung \(x = -1\)
Anmerkung:
Der Definitionsbereich \(D_{f}\) schließt die Nennernullstelle \(x = -1\) aus. Da diese nicht zugleich eine Zählernullstelle ist, ist \(x = -1\) eine Polstelle, an der \(G_{f}\) eine senkrechte Asymptote hat.
Begründung, dass \(G_{f}\) die waagrechte Asymptote \(y = 0\) besitzt
1.Möglichkeit: Zähler- und Nennergrad betrachten
Asymptoten gebrochenrationaler Funktionen
Eine Funktion \(f(x) = \dfrac{z(x)}{n(x)} = \dfrac{\textcolor{#cc071e}{a_{m}}x^{\textcolor{#cc071e}{m}} + a_{m - 1}x^{m - 1} + \dots + a_{1}x +a_{0}}{\textcolor{#0087c1}{b_{n}}x^{\textcolor{#0087c1}{n}} + b_{n - 1}x^{n - 1} + \dots + b_{1}x + b_{0}}\), die sich als Quotient zweier ganzrationaler Funktionen (Polynome) \(z(x)\) und \(n(x)\) darstellen lässt, heißt gebrochenrationale Funktion. Die Nullstellen des Nennerpolynoms \(n(x)\) können nicht in der Definitionsmenge \(D_{f}\) enthalten sein und werden als Definitionslücken bezeichnet.
Senkrechte Asymptoten
Wenn an einer Definitionslücke \(x_{0}\) einer gebrochenrationalen Funktion \(f\)
\(\begin{align*}\lim \limits_{x\,\to\,x_{0}^{-}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{-}}f(x) = -\infty \\[0.8em] \text{und} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = +\infty \enspace &\text{oder} \enspace \lim \limits_{x\,\to\,x_{0}^{+}}f(x) = -\infty \end{align*}\)
gilt, so nennt man \(x_{0}\) eine Polstelle von \(f\) und die Gerade mit der Gleichung \(x = x_{0}\) ist senkrechte Asymptote des Graphen von \(f\).
Waagrechte und schräge Asymptoten
Der Graph einer gebrochenrationalen Funktion \(f\) hat für \(x \to - \infty\) bzw. \(x \to + \infty\) im Fall
| \(\textcolor{#cc071e}{m} < \textcolor{#0087c1}{n}\): | die \(x\)-Achse \((y = 0)\) als waagrechte Asymptote, |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n}\): | eine waagrechte Asymptote parallel zur \(\boldsymbol{x}\)-Achse mit der Gleichung \(y = \dfrac{\textcolor{#cc071e}{a_{m}}}{\textcolor{#0087c1}{b_{n}}}\), |
| \(\textcolor{#cc071e}{m} = \textcolor{#0087c1}{n} + 1\): | eine schräge Asymptote, |
| \(\textcolor{#cc071e}{m} > \textcolor{#0087c1}{n} + 1\): | keine waagrechte oder schräge Asymptote. |
\[f(x) = \frac{\overbrace{4x}^{\large{\text{Grad 1}}}}{\underbrace{(x + 1)^{2}}_{\large{\text{Grad 2}}}}\]
Der Grad des Zählers (Zählerpolynoms) ist kleiner als der Grad des Nenners (Nennerpolynoms). Deshalb ist die Gerade mit der Gleichung \(y = 0\) (\(x\)-Achse) waagrechte Asymptote von \(G_{f}\).
2. Möglichkeit: Grenzwertbtrachtung für \(x \to -\infty\) bzw. \(x \to +\infty\)
Für eine aussagekräftige Grenzwertbetrachtung wird die höchste Potenz des Nenners im Zähler und Nenner ausgeklammert und gekürzt.
\[\begin{align*} \lim \limits_{x\,\to\,-\infty} f(x) &= \lim \limits_{x\,\to\,-\infty} \frac{4x}{\underbrace{(x + 1)^{2}}_{\large{(a\,+\,b)^{2}}}} &&| \; \text{1. Binom. Formel anwenden} \\[0.8em] &= \lim \limits_{x\,\to\,-\infty} \frac{4x}{\underbrace{x^{2} + 2x + 1}_{\large{a^{2}\,+\,2ab\,+\,b^{2}}}} &&| \; x^{2} \; \text{ausklammern und kürzen} \; (x \neq 0) \\[0.8em] &= \lim \limits_{x\,\to\,-\infty} \frac{\cancel{x^{2}} \cdot \frac{4}{x}}{\cancel{x^{2}} \cdot \left( 1 + \frac{2}{x} + \frac{1}{x^{2}} \right)} \\[0.8em] &= \lim \limits_{x\,\to\,-\infty} \frac{\overbrace{\frac{4}{x}}^{\to\,0}}{1 + \underbrace{\frac{2}{x}}_{\to\,0} + \underbrace{\frac{1}{x^{2}}}_{\to\,0}} \\[0.8em] &= 0 \end{align*}\]
analog:
\[\lim \limits_{x\,\to\,+\infty} f(x) = \lim \limits_{x\,\to\,+\infty} \frac{\overbrace{\frac{4}{x}}^{\to\,0}}{1 + \underbrace{\frac{2}{x}}_{\to\,0} + \underbrace{\frac{1}{x^{2}}}_{\to\,0}} = 0\]
Also besitzt \(G_{f}\) die Gerade mit der Gleichung \(y = 0\) als waagrechte Asymptote.

