Im Modell liegt die obere Begrenzungsfläche der wasserführenden Gesteinsschicht in der Ebene \(E\) und die untere Begrenzungsfläche in einer zu \(E\) parallelen Ebene \(F\). Die Ebene \(E\) enthält den Punkt \(Q\). Die Strecke \([PQ]\) steht senkrecht auf der Ebene \(E\) (vgl. Abbildung).
Bestimmen Sie eine Gleichung der Ebene \(E\) in Normalenform.
(zur Kontrolle: \(E \colon 4x_{1} + 4x_{2} - 10x_{3} - 43 = 0\))
(2 BE)
Lösung zu Teilaufgabe c
Da die Strecke \([PQ]\) senkrecht auf der Ebene \(E\) steht, ist der Verbindungsvektor \(\overrightarrow{PQ} = \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix}\) (vgl. Teilaufgabe a) ein Normalenvektor der Ebene \(E\).
Der Punkt \(Q(1|1|-3{,}5) \in E\) dient als Aufpunkt.
1. Möglichkeit: Ansatz mit der Normalenform in Vektordarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
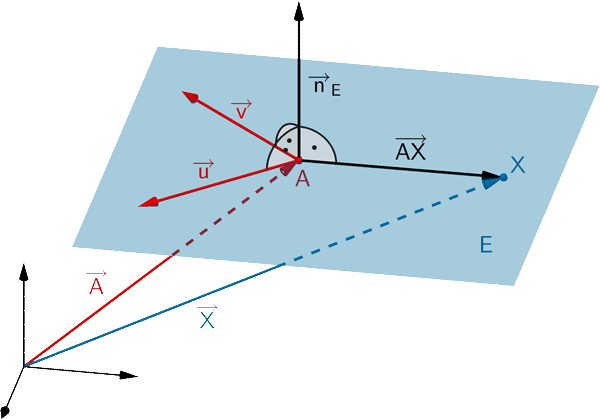
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[\begin{align*}E \colon &\overrightarrow{PQ} \circ (\overrightarrow{X} - \overrightarrow{Q}) = 0 \\[0.8em] E \colon &\begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix} \circ \left[ \overrightarrow{X} - \begin{pmatrix} 1 \\ 1 \\ -3{,}5 \end{pmatrix} \right] = 0 \\[0.8em] &\textcolor{#0087c1}{1 \cdot (x_{1} - 1) + 1 \cdot (x_{2} - 1) - 2{,}5 \cdot (x_{3} + 3{,}5) = 0} \\[0.8em] &\textcolor{#0087c1}{x_{1} - 1 + x_{2} - 1 -2{,}5x_{3} - 10{,}75 = 0} \\[0.8em] \textcolor{#0087c1}{E \colon \,} &\textcolor{#0087c1}{x_{1} + x_{2} - 2{,}5x_{3} - 10{,}75 = 0} \end{align*}\]
Anmerkung:
Da die Aufgabe keine bestimmte Darstellung der Normalenform verlangt, ist das Ausmultiplizieren des Skalarprodukts, d.h. die Umwandlung in die Koordinatendarstellung, nicht unbedingt notwendig.
2. Möglichkeit: Ansatz mit der Normalenform in Koordinatendarstellung
Ebenengleichung in Normalenform (vgl. Merkhilfe)
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]

Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\(\overrightarrow{PQ} = \begin{pmatrix} 1 \\ 1 \\ -2{,}5 \end{pmatrix}\), \(Q(1|1|-3{,}5)\)
\[\begin{align*} &E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0 \\[0.8em] &E \colon 1 \cdot x_{1} + 1 \cdot x_{2} - 2{,}5 \cdot x_{3} + n_{0} = 0 \end{align*}\]
\[\begin{align*} Q \in E \colon 1 \cdot 1 + 1 \cdot 1 - 2{,}5 \cdot (-3{,}5) + n_{0} &= 0 \\[0.8em] 10{,}75 + n_{0} &= 0 &&| - 10{,}75 \\[0.8em] n_{0} &= -10{,}75 \end{align*}\]
\[\Longrightarrow \quad E \colon x_{1} + x_{2} - 2{,}5x_{3} - 10{,}75 = 0\]
Anmerkung:
Durch eine Multiplikation der Ebenengleichung mit dem Faktor 4 (Äquivalenzumformung) erhält man das Kontrollergebnis der Angabe.
\[\begin{align*} &E \colon x_{1} + x_{2} - 2{,}5x_{3} - 10{,}75 = 0 &&| \cdot 4 \\[0.8em] &E \colon 4x_{1} + 4x_{2} - 10x_{3} - 43 = 0 \end{align*}\]

