Ein zweiter Bohrkanal wird benötigt, durch den das entnommene Wasser abgekühlt zurück in die wasserführende Gesteinsschicht geleitet wird. Der Bohrkanal soll geradlinig und senkrecht zur Erdoberfläche verlaufen. Für den Beginn des Bohrkanals an der Erdoberfläche kommen nur Bohrstellen in Betracht, die im Modell durch einen Punkt \(B(t|-t|0)\) mit \(t \in \mathbb R\) beschrieben werden können.
Zeigen Sie rechnerisch, dass der zweite Bohrkanal die wasserführende Gesteinsschicht im Modell im Punkt \(T(t|-t|-4{,}3)\) erreicht, und erläutern Sie, wie die Länge des zweiten Bohrkanals bis zur wasserführenden Gesteinsschicht von der Lage der zugehörigen Bohrstelle beeinflusst wird.
(3 BE)
Lösung zu Teilaufgabe e
\(B(t|-t|0)\), \(T(t|-t|-4{,}3)\) \((t \in \mathbb R)\)
Rechnerischer Nachweis des Punktes \(T(t|-t|4{,}3)\)
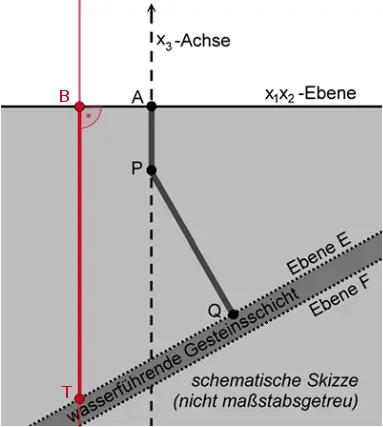
Im Modell verläuft der zweite Bohrkanal entlang der Lotgeraden \(BT\) zur \(x_{1}x_{2}\)-Ebene.
Ein Richtungsvektor der Lotgeraden \(BT\) ist beispielsweise der Vektor \(\overrightarrow{v} = \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\).
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} BT \colon \overrightarrow{X} &= \overrightarrow{B} + \mu \cdot \overrightarrow{v}; \; \mu \in \mathbb R \\[0.8em] BT \colon \overrightarrow{X} &= \begin{pmatrix} t \\ -t \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}; \; \mu \in \mathbb R \end{align*}\]
Der Punkt \(T\) ist der Schnittpunkt der Lotgeraden \(BT\) und der Ebene \(E\) (vgl. Teilaufgabe c).
\[BT \colon \overrightarrow{X} = \begin{pmatrix} t \\ -t \\ 0 \end{pmatrix} + \mu \cdot \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} \textcolor{#cc071e}{t} \\ \textcolor{#0087c1}{-t} \\ \textcolor{#e9b509}{-\mu} \end{pmatrix}; \; \mu \in \mathbb R\]
\[E \colon 4x_{1} + 4x_{2} - 10x_{3} - 43 = 0\]
Für die Bestimmung des Schnittpunkts \(T\) werden die Koordinaten der Gleichung der Lotgeraden \(BT\) in die Gleichung der Ebene \(E\) eingesetzt und diese nach dem Parameter \(\mu\) aufgelöst.
\[\begin{align*} BT \cap E \colon 4 \cdot \textcolor{#cc071e}{t} + 4 \cdot \textcolor{#0087c1}{(-t)} - 10 \cdot \textcolor{#e9b509}{(-\mu)} -43 &= 0 \\[0.8em] 4t - 4t + 10\mu - 43 &= 0 &&| + 43 \\[0.8em] 10\mu &= 43 &&| : 10 \\[0.8em] \mu &= 4{,}3 \end{align*}\]
\(\mu = 4{,}3\) in die Gleichung der Lotgeraden \(BT\) eingesetzt:
\[T \in BT \colon \overrightarrow{T} = \begin{pmatrix} t \\ -t \\ 0 \end{pmatrix} + 4{,}3 \cdot \begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix} = \begin{pmatrix} t \\ -t \\ 4{,}3 \end{pmatrix}\]
\[\Longrightarrow \quad T(t|-t|4{,}3)\]
Also erreicht der zweite Bohrkanal die wasserführende Gesteinsschicht im Modell im Punkt \(T(t|-t|-4{,}3)\).
Einfluss der Lage der zweiten Bohrstelle auf die Länge des zweiten Bohrkanals
Da der zweite Bohrkanal senkrecht zur \(x_{1}x_{2}\)-Ebene verläuft und die \(x_{3}\)-Koordinate von \(T(t|-t|-4{,}3)\) mit \(x_{3} = -4{,}3\) konstant ist, hat der zweite Bohrkanal unabhängigen der Lage der Bohrstelle \(B(t|-t|0)\) in der \(x_{1}x_{2}\)-Ebene stets die Länge 4300 Meter.
oder rechnerisch:
\(B(t|-t| 0)\), \(T(t|-t|4{,}3)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*} \overline{BT} &= \vert| \overrightarrow{BT} \vert| = \vert \overrightarrow{T} - \overrightarrow{B} \vert \\[0.8em] &= \left| \begin{pmatrix} t \\ -t \\ -4{,}3 \end{pmatrix} - \begin{pmatrix} t \\ -t \\ 0 \end{pmatrix} \right| = \left| \begin{pmatrix} 0 \\ 0 \\ -4{,}3 \end{pmatrix} \right| \\[0.8em] &= \sqrt{0^{2} + 0^{2} + (-4{,}3)^{2}} = 4{,}3 \end{align*}\]
Da \(\overline{BT} = 4{,}3\) unabhängig von \(t\) ist, hat die Lage der Bohrstelle \(B(t|-t|0)\) keinen Einfluss auf die Länge des zweiten Bohrkanals.

