- Details
- Kategorie: Geometrie 2
Die Abbildung zeigt den Würfel \(ABCDEFG\) mit \(A(0|0|0)\) und \(G(5|5|5)\) in einem kartesischen Koordinatensystem. Die Ebene \(T\) schneidet die Kanten des Würfels unter anderem in den Punkten \(I(5|0|1)\), \(J(2|5|0)\), \(K(0|5|2)\) und \(L(1|0|5)\).
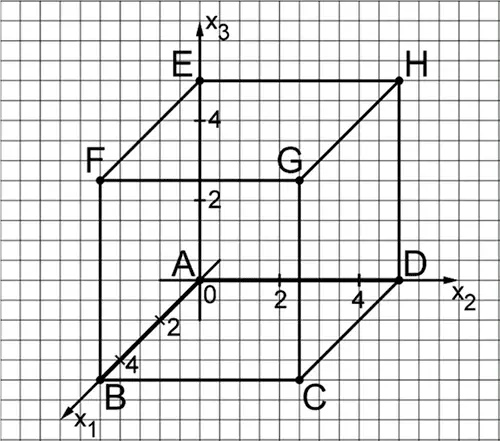
Zeichnen Sie das Viereck \(IJKL\) in die Abbildung ein und zeigen Sie, dass es sich um ein Trapez handelt, bei dem zwei gegenüberliegende Seiten gleich lang sind.
(4 BE)
- Details
- Kategorie: Geometrie 2
Ermitteln Sie eine Gleichung der Ebene \(T\) in Normalenform.
(zur Kontrolle: \(T \colon 5x_{1} + 4x_{2} + 5x_{3} - 30 = 0\))
(3 BE)
- Details
- Kategorie: Geometrie 2
Für \(a \in \mathbb R^{+}\) ist die Gerade \(g_{a} \colon \overrightarrow{X} = \begin{pmatrix} 2{,}5 \\ 0 \\ 3{,}5 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 0 \\ -10a \\ \frac{2}{a} \end{pmatrix}\) mit \(\lambda \in \mathbb R\) gegeben.
Bestimmen Sie den Wert von \(a\), sodass die Gerade \(g_{a}\) die Würfelfläche \(CDHG\) in ihrem Mittelpunkt schneidet.
(3 BE)
- Details
- Kategorie: Geometrie 2
Für jedes \(a \in \mathbb R^{+}\) liegt die Gerade \(g_{a}\) in der Ebene \(U\) mit der Gleichung \(x_{1} = 2{,}5\).
Ein beliebiger Punkt \(P(p_{1}|p_{2}|p_{3})\) des Raums wird an der Ebene \(U\) gespiegelt. Geben Sie die Koordinaten des Bildpunkts \(P'\) in Abhängigkeit von \(p_{1}\), \(p_{2}\) und \(p_{3}\) an.
(2 BE)
- Details
- Kategorie: Geometrie 2
Spiegelt man die Ebene \(T\) an \(U\), so erhält man die von \(T\) verschiedene Ebene \(T'\). Zeigen Sie, dass für einen bestimmten Wert von \(a\) die Gerade \(g_{a}\) in der Ebene \(T\) liegt, und begründen Sie, dass diese Gerade \(g_{a}\) die Schnittgerade von \(T\) und \(T'\) ist.
(4 BE)
- Details
- Kategorie: Geometrie 2
Die Spitze einer Pyramide mit der Grundfläche \(IJKL\) liegt auf der Kante \([FG]\). Untersuchen Sie, ob die Höhe dieser Pyramide 2 betragen kann.
(4 BE)

