Gegeben sind die in \(\mathbb R\) definierten Funktionen \(f \colon x \mapsto x^{2} + 4\) und \(g_{m} \colon x \mapsto m \cdot x\) mit \(m \in \mathbb R\). Der Graph von \(f\) wird mit \(G_{f}\) und der Graph von \(g_{m}\) mit \(G_{m}\) bezeichnet.
Skizzieren Sie \(G_{f}\) in einem Koordinatensystem. Berechnen Sie die Koordinaten des gemeinsamen Punkts der Graphen \(G_{f}\) und \(G_{4}\).
(3 BE)
Lösung zu Teilaufgabe 3a
\[f(x) = x^{2} + 4; \; D_{f} = \mathbb R\]
\[g_{m}(x) = m \cdot x; \; D_{g_{m}} = \mathbb R; \; m \in \mathbb R\]
Skizze von \(G_{f}\)
\(G_{f}\) ist eine um 4 Einheiten in positive \(y\)-Richtung verschobene Normalparabel.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
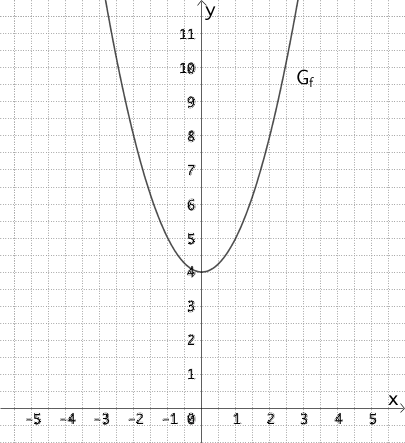
Graph der in \(\mathbb R\) definierten Funktion \(f \colon x \mapsto x^{2} + 4\)
Berechnung der Koordinaten des gemeinsamen Punkts der Graphen \(G_{f}\) und \(G_{4}\)
In der Aufgabenstellung heißt es: „... Koordinaten des gemeinsamen Punkts ...", was auf einen Berührpunkt hinweist.
\[f(x) = x^{2} + 4; \; D_{f} = \mathbb R\]
\[g_{4}(x) = 4 \cdot x; \; D_{g_{4}} = \mathbb R\]
1. Möglichkeit: Funktionsterme gleichsetzen
Für die Berechnung der \(x\)-Koordinate des gemeinsamen Punkts von \(G_{f}\) und \(G_{4}\) werden die Funktionsterme gleichgesetzt und die Gleichung nach \(x\) aufgelöst.
\[\begin{align*} f(x) &= g_{4}(x) \\[0.8em] x^{2} + 4 &= 4x &&| -4x \; \text{(quadratische Gleichung formulieren)} \\[0.8em] \underbrace{x^{2} - 4x + 4}_{a^{2}\,-\,2ab\,+\,b^{2}} &= 0 &&| \; \text{2. Binom. Formel anwenden} \\[0.8em] \underbrace{(x - 2)^{2}}_{(a\,-\,b)^{2}} &= 0 \\[0.8em] x_{1,2} &= 2 \end{align*}\]
Oder mithilfe der Lösungsformel für quadratische Gleichungen (Mitternachtsformel):
\[x^{2} - 4x + 4 = 0\]
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[x_{1,2} = \frac{4 \pm \sqrt{(-4)^{2} - 4 \cdot 1 \cdot 4}}{2 \cdot 1} = \frac{4 \pm \sqrt{0}}{2} = 2\]
\(y\)-Koordinate des gemeinsamen Punkts berechnen:
Hierfür wird \(x = 2\) in einen der beiden Funktionsterme \(f(x)\) oder \(g_{4}(x)\) eingesetzt.
\[g_{4}(2) = 4 \cdot 2 = 8\]
oder
\[f(2) = 2^{2} + 4 = 4 + 4 = 8\]
Somit berühren sich \(G_{f}\) und \(G_{4}\) im Punkt \((2|8)\).
2. Möglichkeit: Differentialrechnung anwenden
Da die Aufgabenstellung auf einen Berührpunkt hinweist, lässt sich dessen \(x\)-Koordinate auch mithilfe der ersten Ableitungen von \(f\) und \(g_{4}\) berechnen.
In einen Berührpunkt haben die beiden sich berührenden Graphen dieselbe Steigung (Steigung der Tangente).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Die erste Ableitung \(f'\) bzw. \(g_{4}'\) beschreibt die Steigung einer Tangente an \(G_{f}\) bzw. \(G_{4}\). Somit gilt im Berührpunkt: \(f'(x) = g_{4}'(x)\).

Ableitungen der Grundfunktionen
\[c' = 0 \enspace (c \in \mathbb R)\]
\[\left( x^r \right)' = r \cdot x^{r - 1} \enspace (r \in \mathbb R)\]
\[\left( \sqrt{x} \right)' = \frac{1}{2\sqrt{x}}\]
\[\left( \sin{x} \right)' = \cos{x}\]
\[\left( \cos{x} \right)' = -\sin{x}\]
\[\left( \ln{x} \right)' = \frac{1}{x}\]
\[\left( \log_{a}{x}\right)' = \frac{1}{x \cdot \ln{a}}\]
\[\left( e^x \right)' = e^x\]
\[\left(a^x \right)' = a^x \cdot \ln{a}\]
vgl. Merkhilfe
Faktorregel
\[\begin{align*}f(x) &= a \cdot \textcolor{#0087c1}{u(x)} \\[0.8em] f'(x) &= a \cdot \textcolor{#0087c1}{u'(x)}\end{align*}\]
Summenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} + \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} + \textcolor{#cc071e}{v'(x)}\end{align*}\]
Produktregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v(x)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} + \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
Quotientenregel
\[\begin{align*}f(x) &= \dfrac{\textcolor{#0087c1}{u(x)}}{\textcolor{#cc071e}{v(x)}} \\[0.8em] f'(x) &= \dfrac{\textcolor{#0087c1}{u'(x)} \cdot \textcolor{#cc071e}{v(x)} - \textcolor{#0087c1}{u(x)} \cdot \textcolor{#cc071e}{v'(x)}}{[\textcolor{#cc071e}{v(x)}]^{2}}\end{align*}\]
Kettenregel
\[\begin{align*}f(x) &= \textcolor{#0087c1}{u(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \\[0.8em] f'(x) &= \textcolor{#0087c1}{u'(}\textcolor{#cc071e}{v(x)}\textcolor{#0087c1}{)} \cdot \textcolor{#cc071e}{v'(x)}\end{align*}\]
vgl. Merkhilfe
\[f(x) = x^{2} + 4 \quad \Longrightarrow \quad f'(x) = 2x\]
\[g_{4}(x) = 4x \quad \Longrightarrow \quad g_{4}'(x) = 4\]
\[f'(x) = g_{4}'(x) \quad \Longleftrightarrow \quad 2x = 4 \quad \Longleftrightarrow \quad x = 2\]
Die Berechnung der \(y\)-Koordinate erfolgt wie unter 1. Möglichkeit beschrieben.

