Gegeben ist die Funktion \(g \colon x \mapsto \ln{(2 - x^{2})}\) mit maximaler Definitionsmenge \(D_{g}\).
Skizzieren Sie die Parabel mit der Gleichung \(y = 2 - x^{2}\) in einem Koordinatensystem und geben Sie \(D_{g}\) an.
(3 BE)
Lösung zu Teilaufgabe 1a
\[g(x) = \ln{(2 - x^{2})}\]
Skizze der Parabel mit der Gleichung \(y = 2 - x^{2}\)
\[y = 2 - x^{2} = \textcolor{#cc071e}{\mathbf{-}}x^{2} \textcolor{#0087c1}{+ 2}\]
Es handelt sich um eine nach unten geöffnete (Öffnungsfaktor - 1) und um 2 Einheiten in positive \(y\)-Richtung verschobene Normalparabel.
Verschieben von Funktionsgraphen
\[g(x) = f(x +a) + b\]
Verschiebung in \(x\)-Richtung um \(-a\), Verschiebung in \(y\)-Richtung um \(b\)
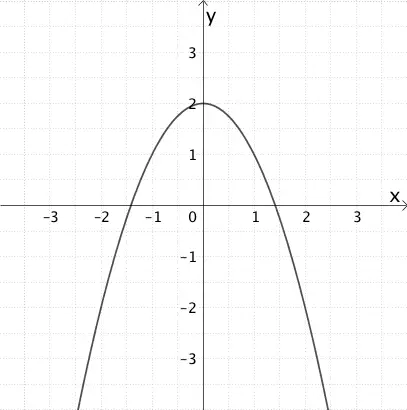
Parabel mit der Gleichung \(y = 2 - x^{2}\)
Maximale Definitionsmenge \(D_{g}\)
\[D_{g} =\; ]-\sqrt{2};\sqrt{2}[\]
1. Halbgraphische Begründung (nicht verlangt)
\[g(x) = \ln{(\underbrace{2 - x^{2}}_{\textcolor{#0087c1}{\large{>\,0}}})}\]
Maximale Definitionsmenge bestimmen
Gebrochenrationale Funktion / Quotient von Funktionen
\[x \mapsto \dfrac{Zähler(x)}{\textcolor{#e9b509}{\underbrace{Nenner(x)}_{\Large{\neq \, 0}}}}\]
Nullstelle(n) des Nenners ausschließen!
Wurzelfunktion
\[x \mapsto \sqrt{\mathstrut\smash{\textcolor{#e9b509}{\underbrace{\dots}_{\Large{\geq\,0}}}}} \\ {}\]
Der Wert des Terms unter der Wurzel (Radikand ) darf nicht negativ sein!
(natürliche) Logarithmusfunktion
\(x \mapsto \ln{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\) bzw. \(x \mapsto \log_{a}{(\,\textcolor{#e9b509}{\underbrace{\dots}_{\Large{>\,0}}}\,)}\)
Die (Natürliche) Logarithmusfunktion ist in \(\textcolor{#e9b509}{\mathbb R^{+}}\) definiert!
Die (natürliche) Logarithmusfunktion ist in \(\textcolor{#0087c1}{\mathbb R^{+}}\) definiert.
Die Skizze der Parabel mit der Gleichung \(y = 2 - x^{2}\) zeigt, dass die Parabel zwischen deren Nullstellen oberhalb der \(x\)-Achse (im Positiven) verläuft.
Nullstellen der Parabel berechnen:
\[\begin{align*} 2 - x^{2} &= 0 &&| + x^{2} \\[0.8em] 2 &= x^{2} &&| \; \sqrt{\quad} \\[0.8em] \pm\sqrt{2} &= x_{1,2}\end{align*}\]
\[\Longrightarrow \quad D_{g} =\; \textcolor{#0087c1}{]-\sqrt{2};\sqrt{2}[}\]
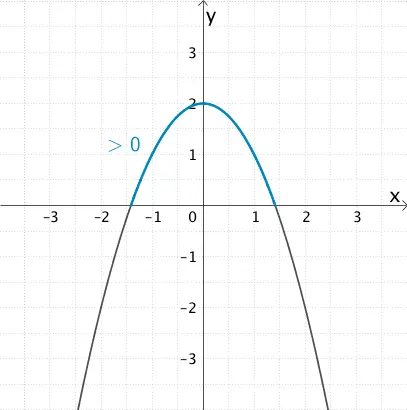
2. Rechnerische Begründung (nicht verlangt)
\[\begin{align*} 2 - x^{2} &> 0 &&| + x^{2} \\[0.8em] 2 &> x^{2} &&| \; \sqrt{\quad}\; \text{wobei} \; \sqrt{a^{2}} = \vert a \vert \; \text{mit} \; a \in \mathbb R \; \text{gilt} \\[0.8em] \sqrt{2} &> \vert x \vert \end{align*}\]
Die Betragsungleichung lässt sich durch Fallunterscheidung lösen.
1. Fall: \(x \geq 0\)
Für \(x \geq 0\) können die Betragsstriche entfallen.
\[\Longrightarrow \quad x < \sqrt{2}\]
2. Fall: \(x < 0\)
Für \(x < 0\) kann \(\vert x \vert\) durch \(-x\) ersetzt werden.
\[\begin{align*}\Longrightarrow \quad - x &< \sqrt{2} &&| \cdot (-1) \; \textcolor{#cc071e}{\text{Relationszeichen dreht sich!}} \\[0.8em] x &\textcolor{#cc071e}{>} -\sqrt{2}\end{align*}\]
\[\Longrightarrow \quad -\sqrt{2} < x < \sqrt{2}\]
\[\Longrightarrow \quad D_{g} = \;]-\sqrt{2};\sqrt{2}[\]

