Die Abbildung 2 zeigt den Graphen \(G_{f}\) einer in \([0{,}8; +\infty[\) definierten Funktion f.
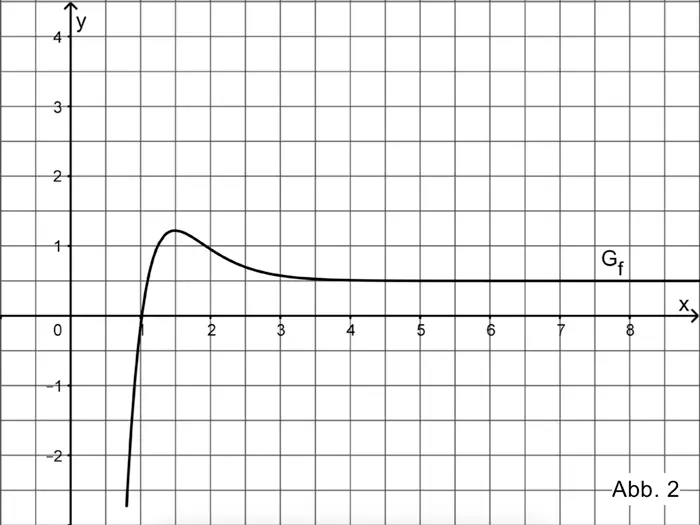
Betrachtet wird zudem die in \([0{,}8; +\infty[\) definierte Integralfunktion \(\displaystyle J \colon x \mapsto \int_{2}^{x} f(t) dt\).
Begründen Sie mithilfe von Abbildung 2, dass \(J(1) \approx -1\) gilt, und geben Sie einen Näherungswert für den Funktionswert \(J(4{,}5)\) an. Skizzieren Sie den Graphen von \(J\) in der Abbildung 2.
(5 BE)
Lösung zu Teilaufgabe 4
\[J(x) = \int_{2}^{x}f(t)dt\]
Begründung mithilfe von Abbildung 2, dass \(J(1) \approx -1\) gilt
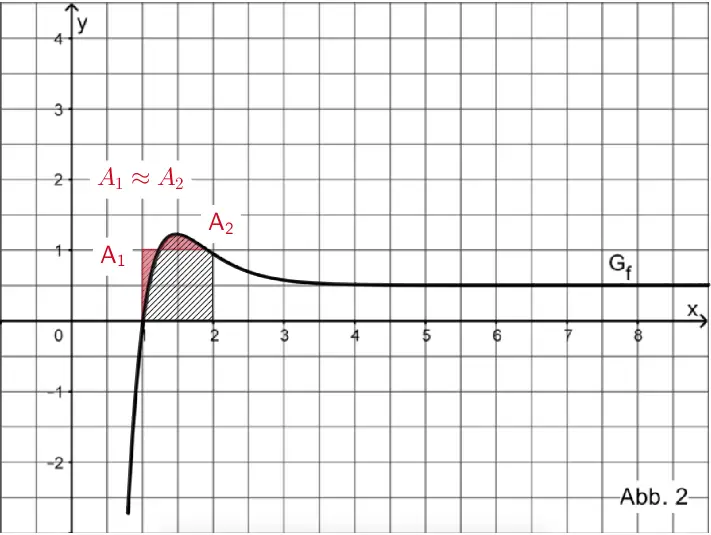
Das bestimmte Integral \(\displaystyle \int_{1}^{2}f(t)dt\) errechnet die Maßzahl des Flächeninhalts des Flächenstücks, welches \(G_{f}\) im Intervall \([1;2]\) mit der \(x\)-Achse einschließt. Dieses Flächenstück ist näherungsweise flächeninhaltsgleich einem Quadrat mit dem Flächeninhalt 1 FE (4 Kästchen a 0,25 FE), das in \(x\)-Richtung im selben Maße um \(\textcolor{#cc071e}{A_{1}}\) zu groß ist wie es in \(y\)-Richtung um \(\textcolor{#cc071e}{A_{2}}\) zu klein ist \((\textcolor{#cc071e}{A_{1} \approx A_{2}})\).
\[\Longrightarrow \quad \int_{1}^{2}f(t)dt \approx 1\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Da \(G_{f}\) im Bereich \(1 \leq x \leq 2\) oberhalb der \(x\)-Achse verläuft, aber mit \(\displaystyle J(1) = \int_{2}^{1}f(t)dt\) „nach links" integriert wird, bzw. weil \(\displaystyle J(1) = \int_{2}^{1}f(t) = -\int_{1}^{2}f(t)dt\) gilt (Vertauschungsregel), ist der Funktionswert \(J(1)\) negativ.
\[\Longrightarrow \quad J(1) = \int_{2}^{1}f(t)dt = -\int_{1}^{2}f(t)dt \approx -1\]
Näherungswert für den Funktionswert \(J(4{,}5)\)
\[J(4{,}5) \approx 1{,}5\]
Begründung (nicht verlangt)
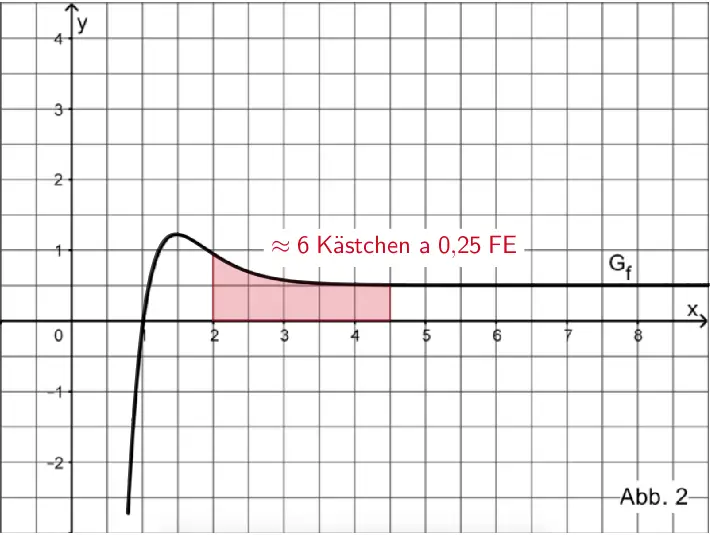
Das bestimmte Integral \(\displaystyle J(4{,}5) = \int_{2}^{4{,}5}f(t)dt\) errechnet die Maßzahl des Flächeninhalts des Flächenstücks, welches \(G_{f}\) im Intervall \([2;4{,}5]\) mit der \(x\)-Achse einschließt. Da \(G_{f}\) im Bereich \(2 \leq x \leq 4{,}5\) oberhalb der \(x\)-Achse verläuft, ist der Funktionswert \(J(4{,}5)\) positiv.
Durch „Kästchen zählen" ergibt sich näherungsweise:
\[J(4{,}5) = \int_{2}^{4{,}5}f(t)dt \approx 6 \cdot 0{,}25 = 1{,}5\]
Skizze des Graphen von \(J\) in Abbildung 2
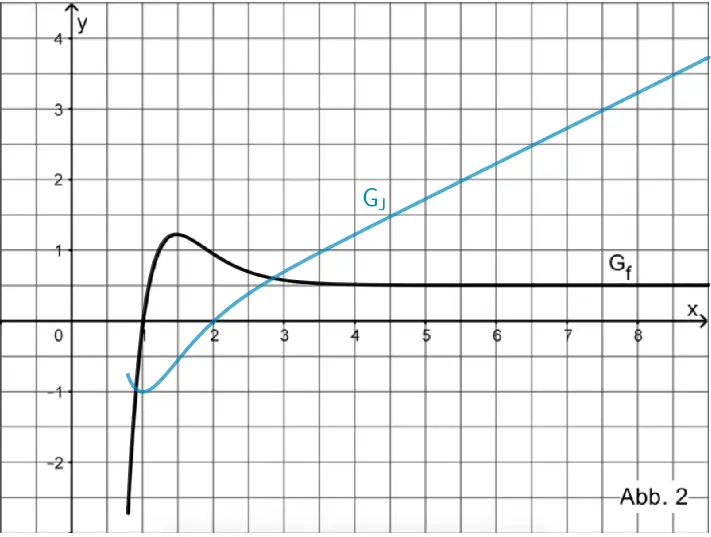
Verlauf des Graphen der Integralfunktion \(\displaystyle J(x) = \int_{2}^{x}f(t)dt; \; D_{J} = [0{,}8;+\infty[\)
Ausführliche Erklärung (nicht verlangt)
Für das Skizzieren des Graphen der Integralfunktion \(J\) eignet sich insbesondere
- die Betrachtung der Nullstelle von \(G_{f}\),
- die Betrachtung des Hochpunkts von \(G_{f}\),
- die Betrachtung der Nullstelle von \(J\) sowie
- die Betrachtung des asymptotischen Verlaufs von \(G_{f}\) für \(x \to +\infty\).
Betrachtung der Nullstelle von \(G_{f}\)
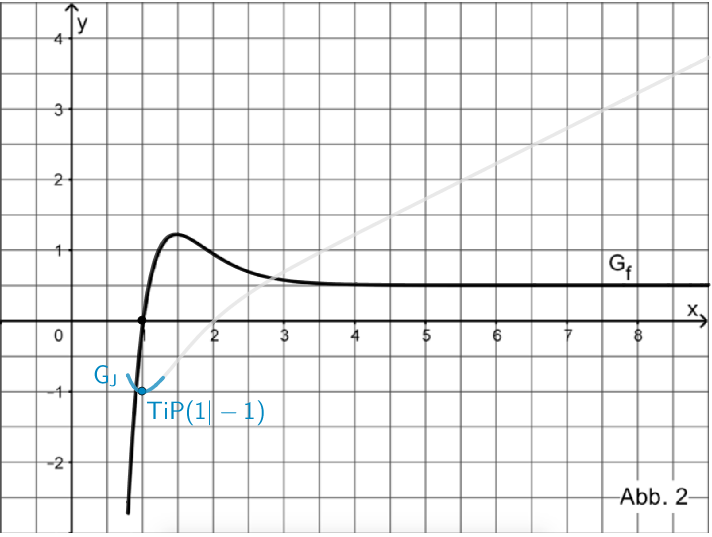
Abbildung 2 zeigt, dass \(x \approx 1\) eine Nullstelle von \(G_{f}\) ist.
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung, ist die Integralfunktion \(J\) eine Stammfunktion der Funktion \(f\) und es gilt näherungsweise:
Stammfunktion
Eine differenzierbare Funktion \(F(x)\) heißt eine Stammfunktion von \(f(x)\), wenn
\(F'(x) = f(x)\) mit \(D_{F} = D_{f}\)
gilt.
\[J'(1) = f(1) = 0\]
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Folglich hat \(\textcolor{#0087c1}{G_{J}}\) an der Stelle \(x \approx 1\) eine waagrechte Tangente (Tangentensteigung ist Null).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Da \(x \approx 1\) zudem eine Nullstelle von \(f\) mit Vorzeichenwechsel von \(-\) nach \(+\) ist, folgt mithilfe des Monotoniekriteriums, dass \(\textcolor{#0087c1}{G_{J}}\) an der Stelle \(x \approx 1\) das Monotonieverhalten von „streng monoton fallend" nach „streng monoton steigend" wechselt. Also hat \(\textcolor{#0087c1}{G_{J}}\) an der Stelle \(x \approx 1\) einen Tiefpunkt.
Mit \(J(1) \approx -1\) (vgl. oben) folgt: Tiefpunkt \(TiP(1|-1)\).
\[\left. \begin{align*} &f(x) = J'(x) < 0 \enspace \text{für} \enspace x < 1 \\ &f(1) = J'(1) = 0 \\ &f(x) = J'(x) > 0 \enspace \text{für} \enspace x > 1 \end{align*} \right \} \enspace \Rightarrow \enspace \textcolor{#0087c1}{\text{Tiefpunkt} \; TiP\,(1|J(-1))}\]
Wegen des eingeschränkten Definitionsbereichs \(D_{J} = [0{,}8;+\infty[\) beginnt der Verlauf des Graphen \(G_{J}\) an der Stelle \(x = 0{,}8\).
Betrachtung des Hochpunkts von \(G_{f}\)
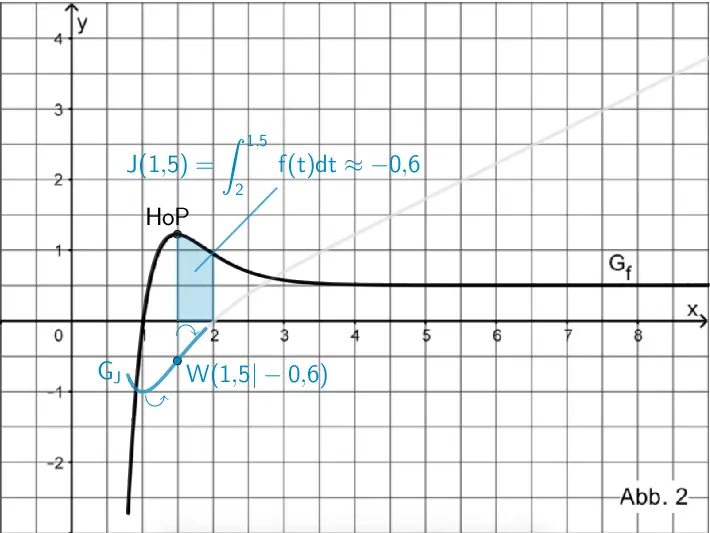
Gemäß Abbildung 2 besitzt \(G_{f}\) an der Stelle \(x \approx 1{,}5\) einen Hochpunkt.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Im Hochpunkt hat \(G_{f}\) die Steigung Null (Steigung einer Tangente an \(G_{f}\) ist Null, waagrechte Tangente). Da \(f'\) die Steigung von \(G_{f}\) beschreibt und nach dem Hauptsatz der Differntial- und Integralrechnung \(J'(x) = f(x)\) bzw. \(J''(x) = f'(x)\) gilt, folgt näherungsweise:
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
\[J''(1{,}5) = f'(1{,}5) = 0\]
Anwendung der Differentialrechnung:
Krümmungsverhalten von Funktionsgraphen
\(f''(x) < 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) rechtsgekrümmt.
\(f''(x) > 0\) im Intervall \(I \quad \Longrightarrow \quad G_f\) ist in \(I\) linksgekrümmt.
(vgl. Merkhilfe)
Da sich in der Umgebung des Hochpunkts von \(G_{f}\) die Steigung von „positiv" \(f'(x) = J''(x) > 0\) nach „negativ" \(f'(x) = J''(x) < 0\) ändert, wechselt \(\textcolor{#0087c1}{G_{J}}\) an der Stelle \(x \approx 1{,}5\) das Krümmungsverhalten von linksgekrümmt \(\style{display: inline-block; transform:rotate(0.5turn);}{ \textcolor{#0087c1}{\curvearrowleft}}\) nach rechtsgekrümmt \(\textcolor{#0087c1}{\curvearrowright}\). Also hat \(\textcolor{#0087c1}{G_{J}}\) an der Stelle \(x \approx 1{,}5\) einen Wendepunkt.
Anwendung der Differetialrechnung:
Wendepunkt
Ist \(f''(x_0) = 0\) und wechselt \(f''\) an der Stelle \(x_0\) das Vorzeichen, so hat \(G_f\) an der Stelle \(x_0\) einen Wendepunkt.
(vgl. Merkhilfe)
Alternative:
Es muss \(f''(x_{0}) = 0\) und \(f'''(x_{0}) \neq 0\) gelten.
\[\left. \begin{align*} &f'(x) = J''(x) > 0 \enspace \text{für} \enspace x < 1{,}5 \\ &f'(1{,}5) = J''(1{,}5) = 0 \\ &f'(x) = J''(x) < 0 \enspace \text{für} \enspace x > 1{,}5 \end{align*} \right \} \enspace \Rightarrow \enspace \textcolor{#0087c1}{\text{Wendepunkt} \; W\,(1{,}5|J(1{,}5))}\]
Die \(y\)-Koordinate des Wendepunkts lässt sich näherungsweise mithilfe von \(G_{f}\) berechnen.
Das Flächenstück, das \(G_{f}\) im Intervall \([1{,}5;2]\) mit der \(x\)-Achse einschließt ist ca. 2,25 Kästchen a 0,25 FE groß. Damit ergibt sich:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*}J(1{,}5) &= \int_{2}^{1{,}5}f(t)dt \\[0.8em] &= - \textcolor{#0087c1}{\int_{1{,}5}^{2}f(t)dt} \\[0.8em] &\approx - \textcolor{#0087c1}{2{,}25 \cdot 0{,}25} \\[0.8em] &\approx -0{,}6\end{align*}\]
\[\Longrightarrow \quad \textcolor{#0087c1}{W(1{,}5)|-0{,}6)}\]
Betrachtung der Nullstelle von \(J\)
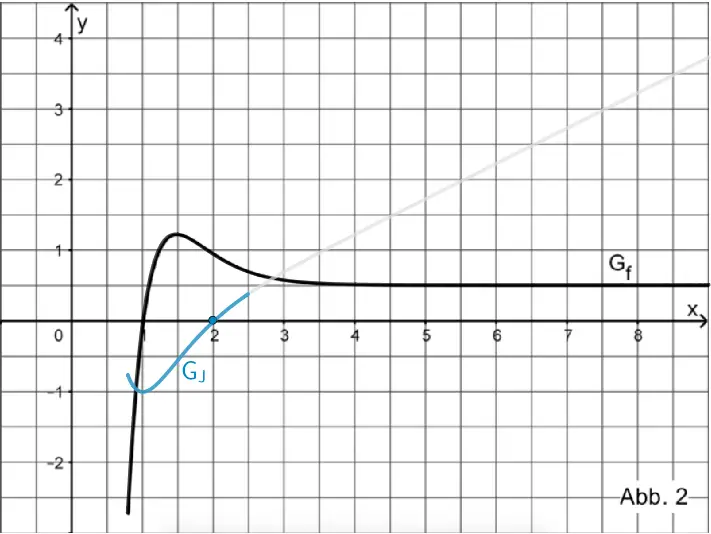
Jede Integralfunktion hat an der unteren Integrationsgrenze eine Nullstelle. Somit hat die Integralfunktion \(\displaystyle J(x) = \int_{2}^{x}f(t)dt\) die Nullstelle \(x = 2\).
Nullstelle einer Integralfunktion
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) besitzt an der unteren Integrationsgrenze \(x = a\) eine Nullstelle.
\[I_{a}(a) = \int_{a}^{a} f(t) \, dt = F(a) - F(a) = 0\]
\(F\) ist eine Stammfunktion von \(f\).
\[J(2) = \int_{2}^{2}f(t)dt = F(2) - F(2) = 0\]
Betrachtung des asymptotischen Verlaufs von \(G_{f}\) für \(x \to +\infty\)
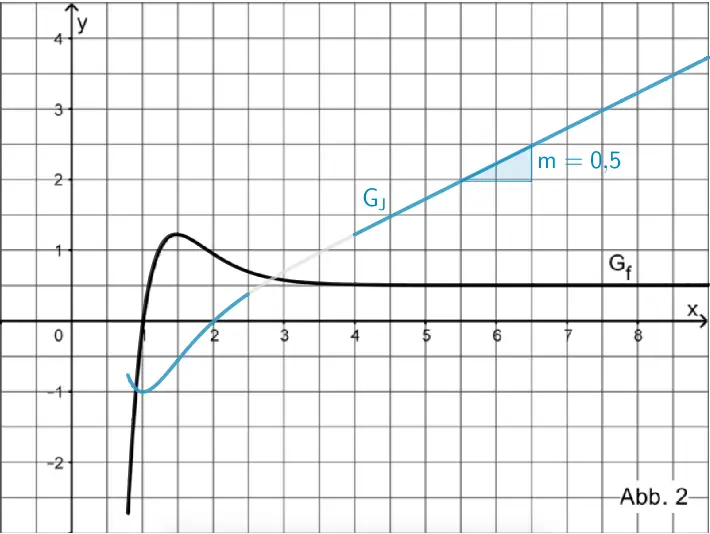
Für \(x \to +\infty\) nähert sich \(G_{f}\) der waagrechten Asymptote mit der Gleichung \(y = 0{,}5\) an.
Hauptsatz der Differential- und Integralrechnung (HDI)
Jede Integralfunktion \(\displaystyle I_{a} \colon x \mapsto \int_{a}^{x} f(t)\, dt\) einer stetigen Funktion \(f\) ist eine Stammfunktion von \(f\).
\[I_{a}(x) = \int_{a}^{x} f(t)\, dt \quad \Longrightarrow \quad I'_{a}(x) = f(x)\]
(vgl. Merkhilfe)
Nach dem Hauptsatz der Differential- und Integralrechnung gilt \(f(x) = J'(x)\). Insbesondere gilt für \(x \to +\infty\) somit \(f(x) = J'(x) = 0{,}5\).
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Da \(J'(x)\) die Steigung von \(G_{J}\) (Steigung einer Tangente an \(G_{J}\)) beschreibt, verläuft \(G_{J}\) ab \(x \approx 4\) näherungsweise wie eine Gerade mit der konstanten Steigung \(m = 0{,}5\).
Zusammenfassung
Der Graph \(G_{J}\) der Integralfunktion \(J\) hat
- näherungsweise den Tiefpunkt \(TiP(1|-1)\),
- näherungsweise den Wendepunkt \(W(1{,}5|-0{,}6)\),
- genau die Nullstelle \(x = 2\) sowie
- näherungsweise ab \(x \approx 4\) den Verlauf einer Geraden mit der Steigung \(m = 0{,}5\).
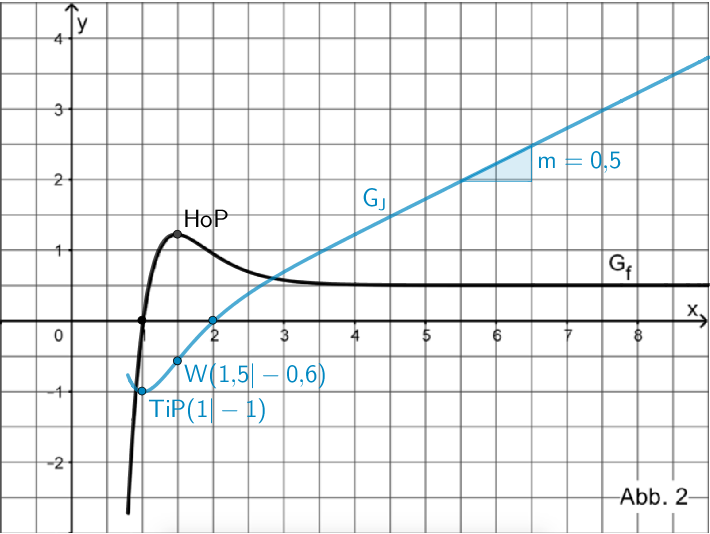
Verlauf des Graphen der in \([0{,}8;+\infty[\) definierten Integralfunktion \(\displaystyle J \colon x \mapsto \int_{2}^{x}f(t)dt\) mit Tiefpunkt \(TiP(1|-1)\), Wendepunkt \(W(1{,}5|-0{,}6)\), Nullstelle \(x = 2\) und konstanter Steigung \(m = 0{,}5\) für \(x \to +\infty\).

