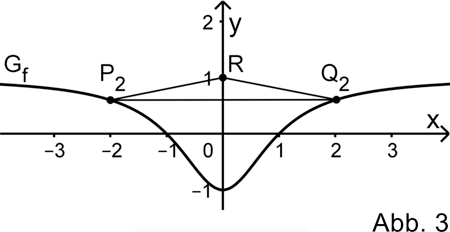
Für jeden Wert \(k > 0\) legen die auf \(G_{f}\) liegenden Punkte \(P_{k}(-k|f(-k))\) und \(Q_{k}(k|f(k))\) gemeinsam mit dem Punkt \(R(0|1)\) ein gleichschenkliges Dreieck \(P_{k}Q_{k}R\) fest.
Berechnen Sie für \(k = 2\) den Flächeninhalt des zugehörigen Dreiecks \(P_{2}Q_{2}R\) (vgl. Abbildung 3).
Zeigen Sie anschließend, dass der Flächeninhalt des Dreiecks \(P_{k}Q_{k}R\) allgemein durch den Term \(A(k) = \dfrac{2k}{k^{2} + 1}\) beschrieben werden kann.
(5 BE)
Lösung zu Teilaufgabe 3a
\(P_{k}(-k|f(-k))\), \(Q_{k}(k|f(k))\) mit \(k > 0\), \(R(0|1)\)
Flächeninhalt des Dreiecks \(P_{2}Q_{2}R\)
![Dreieck P₂Q₂R mit Grundlinie [P₂Q₂] und Höhe 1 - f(2)](/images/stories/B2020_PT_B_A1/B2020_PT_B_A1_3a.png)
Dreieck \(P_{2}Q_{2}R\) mit Grundlinienlänge \(\textcolor{#cc071e}{4}\) und Höhe \(\textcolor{#e9b509}{1 - f(2)}\)
Für \(k = 2\): \(P_{2}(-2|f(-2))\) und \(Q_{2}(2|f(2))\) sowie \(R(0|1)\)
\[f(x) = \frac{x^{2} - 1}{x^{2} + 1}; \; D_{f} = \mathbb R\]
\[\begin{align*} A_{P_{2}Q_{2}R} &= \frac{1}{2} \cdot \textcolor{#cc071e}{g} \cdot \textcolor{#e9b509}{h} \\[0.8em] &= \frac{1}{2} \cdot \textcolor{#cc071e}{(x_{Q_{2}} - x_{P_{2}})} \cdot \textcolor{#e9b509}{(1 - f(2))} \\[0.8em] &= \frac{1}{2} \cdot \textcolor{#cc071e}{(2 - (-2))} \cdot \textcolor{#e9b509}{\left(1 - \frac{2^{2} - 1}{2^{2} + 1}\right)} \\[0.8em] &= \frac{1}{2} \cdot \textcolor{#cc071e}{4} \cdot \textcolor{#e9b509}{\left( 1 - \frac{3}{5} \right)} \\[0.8em] &= 2 \cdot \frac{2}{5} \\[0.8em] &= \frac{4}{5} = 0{,}8 \end{align*}\]
Der Flächeninhalt des Dreiecks \(P_{2}Q_{2}R\) beträgt 0,8 FE (Flächeneinheiten).
Nachweis, dass der Flächeninhalt des Dreiecks \(P_{k}Q_{k}R\) durch den Term \(A(k) = \dfrac{2k}{k^{2} + 1}\) beschrieben werden kann
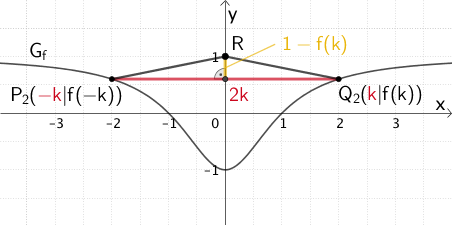
Dreieck \(P_{k}Q_{k}R\) mit Grundlinienlänge \(\textcolor{#cc071e}{2k}\) und Höhe \(\textcolor{#e9b509}{1 - f(k)}\)
\(P_{k}(-k|f(-k))\), \(Q_{k}(k|f(k))\) mit \(k > 0\), \(R(0|1)\)
\[f(x) = \frac{x^{2} - 1}{x^{2} + 1}; \; D_{f} = \mathbb R\]
\[\begin{align*} A(k) &= \frac{1}{2} \cdot \textcolor{#cc071e}{g} \cdot \textcolor{#e9b509}{h} \\[0.8em] &= \frac{1}{2} \cdot \textcolor{#cc071e}{(x_{Q_{k}} - x_{P_{k}})} \cdot \textcolor{#e9b509}{(1 - f(k))} \\[0.8em] &= \frac{1}{2} \cdot \textcolor{#cc071e}{(k - (-k))} \cdot \textcolor{#e9b509}{\left(1 - \frac{k^{2} - 1}{k^{2} + 1}\right)} &&| \; \text{gemeinsamer Nenner}\; k^{2} + 1 \\[0.8em] &= \frac{1}{2} \cdot \textcolor{#cc071e}{2k} \cdot \textcolor{#e9b509}{\left( \frac{k^{2} + 1}{k^{2} + 1} - \frac{k^{2} - 1}{k^{2} + 1} \right)} \\[0.8em] &= k \cdot \frac{k^{2} + 1 - (k^{2} - 1)}{k^{2} + 1} \\[0.8em] &= k \cdot \frac{2}{k^{2} + 1} \\[0.8em] &= \frac{2k}{k^{2} + 1}\end{align*}\]

