Berechnen Sie den Inhalt des Flächenstücks, das von \(G_{f}\), der \(y\)-Achse sowie den Geraden mit den Gleichungen \(y = 1\) und \(x = 5\) begrenzt wird. Einen Teil dieses Flächenstücks nimmt das zu \(s = 5\) gehörige Rechteck ein. Bestimmen Sie den prozentualen Anteil des Flächeninhalts dieses Rechtecks am Inhalt des Flächenstücks.
(7 BE)
Lösung zu Teilaufgabe 1c
\[f(x) = 1 + 7e^{-0{,}2x}; \; D_{f} = \mathbb R_{0}^{+}\]
Berechnung des Inhalt des Flächenstücks, das von \(G_{f}\), der \(y\)-Achse sowie den Geraden mit den Gleichungen \(y = 1\) und \(x = 5\) begrenzt wird
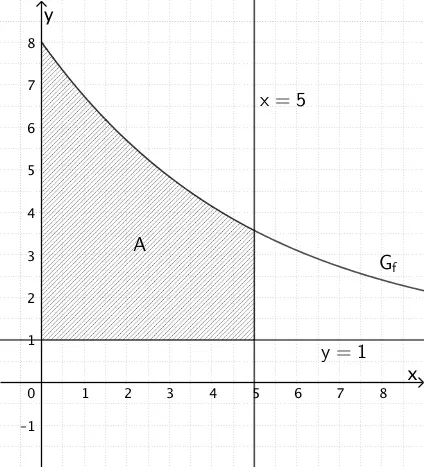
Flächeninhalt \(A\) des Flächenstücks, welches \(G_{f}\), die \(y\)-Achse sowie die Geraden mit den Gleichungen \(y = 1\) und \(x = 5\) einschließen.
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} A &= \int_{0}^{5}(f(x) - 1)dx \\[0.8em] &= \int_{0}^{5}\left( 1 + 7e^{-0{,}2x} - 1 \right)dx \\[0.8em] &= \int_{0}^{5}7e^{-0{,}2x}dx \\[0.8em] &= \bigg[ \underbrace{7 \cdot \frac{1}{-0{,}2} \cdot e^{-0{,}2x}}_{\text{Stammfunktion}} \bigg]_{\textcolor{#89ba17}{0}}^{\textcolor{#e9b509}{5}} \\[0.8em] &= \left[ -35 \cdot e^{-0{,}2x} \right]_{\textcolor{#89ba17}{0}}^{\textcolor{#e9b509}{5}} \\[0.8em] &= -35 \cdot e^{-0{,}2 \cdot \textcolor{#e9b509}{5}} - \big( -35 \cdot \underbrace{e^{-0{,}2 \cdot \textcolor{#89ba17}{0}}}_{1} \big) \\[0.8em] &= -35 \cdot e^{-1} + 35 &&|\; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= 35 - \frac{35}{e} \\[0.8em] &= 35 \cdot \left( 1 - \frac{1}{e} \right) \\[0.8em] &= 35 \cdot \frac{e - 1}{e} \\[0.8em] &\approx 22{,}12 \end{align*}\]
Der Flächeninhalt des Flächenstücks, das von \(G_{f}\), der \(y\)-Achse sowie den Geraden mit den Gleichungen \(y = 1\) und \(x = 5\) begrenzt wird, beträgt ca. 22,12 FE (Flächeneinheiten).
Ausführliche Erklärung (nicht verlangt)

Das Flächenstück mit dem Flächeninhalt \(A\) wird in \(y\)-Richtung durch \(G_{f}\) und die Gerade mit der Gleichung \(y = 1\) begrenzt. Der Flächeninhalt \(A\) lässt sich somit durch Integration über die Differenzfunktion \(f(x) - 1\) berechnen.
\[\begin{align*} A &= \int_{0}^{5}(f(x) - 1)dx \\[0.8em] &= \int_{0}^{5}\left( 1 + 7e^{-0{,}2x} - 1 \right)dx \\[0.8em] &= \int_{0}^{5}7e^{-0{,}2x}dx\end{align*}\]
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
Für die Berechnung des bestimmten Integrals \(\displaystyle \int_{0}^{5}7e^{-0{,}2x}dx\) wird eine Stammfunktion der Integrandenfunktion \(x \mapsto 7e^{-0{,}2x}\) benötigt.
Die Menge aller Stammfunktionen der Integrandenfunktion \(x \mapsto 7e^{-0{,}2x}\) ist gegeben durch das unbestimmte Integral \(\displaystyle \int 7e^{-0{,}2x}dx\).
Mithilfe der unbestimmten Integrale
\(\displaystyle \textcolor{#cc071e}{\int e^{x} dx = e^{x} + C}\) und
\(\displaystyle \textcolor{#0087c1}{\int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C}\)
ergibt sich:
Wichtige unbestimmte Integrale (\(C \in \mathbb R\), vgl. Merkhilfe)
\[\int x^{r} dx = \frac{x^{r + 1}}{r + 1} + C \quad (r \neq - 1)\]
\[\int \frac{1}{x}\,dx = \ln{\vert x \vert} + C\]
\[\int \sin{x} \, dx = -\cos{x} + C\]
\[\int \cos{x} \, dx = \sin{x} + C\]
\[\int e^{x} dx = e^{x} + C\]
\[\int \ln{x}\, dx = -x + x \cdot \ln{x} + C\]
\[\int \frac{f'(x)}{f(x)} dx = \ln{\vert f(x) \vert} + C\]
\[\int f'(x) \cdot e^{f(x)} dx = e^{f(x)} + C\]
\(\displaystyle \int f(ax + b) \, dx = \frac{1}{a} \cdot F(ax + b) + C\), wobei \(F\) eine Stammfunktion von \(f\) ist.
Es gilt die Faktorregel und die Summenregel:
\(\displaystyle \int c \cdot f(x)\,dx = c \cdot \int f(x)\,dx\) mit \(c \in \mathbb R\)
\( \displaystyle \int \left[f(x) \pm g(x) \right] dx = \int f(x)\,dx \pm \int g(x)\,dx\)
\[\begin{align*}\int 7\textcolor{#cc071e}{e}^{\textcolor{#0087c1}{-0{,}2x}} &= 7 \cdot \textcolor{#0087c1}{\frac{1}{-0{,}2}} \cdot \textcolor{#cc071e}{e}^{\textcolor{#0087c1}{-0{,}2x}} + C \\[0.8em] &= -35 \cdot e^{-0{,}2x} + C\end{align*}\]
Somit ist \(x \mapsto -35 \cdot e^{-0{,}2x}\) eine Stammfunktion der Integrandenfunktion \(x \mapsto 7e^{-0{,}2x}\) (für \(C = 0\)) und es folgt:
Berechnung bestimmter Integrale
\[\int_{a}^{b} f(x)\,dx = [F(x)]_{a}^{b} = F(b) - F(a)\]
Dabei ist \(F\) eine beliebige Stammfunktion zu \(f\).
(vgl. Merkhilfe)
Eigenschaften des bestimmten Integrals - Integrationsregeln
Identische Integrationsgrenzen:
\[\int_{a}^{a} f(x)\,dx = 0\]
Faktorregel:
\(\displaystyle \int_{a}^{b} c \cdot f(x)\,dx = c \cdot \int_{a}^{b} f(x)\,dx\) mit \(c \in \mathbb R\)
Summenregel:
\[\int_{a}^{b} \left[f(x) \pm g(x) \right] dx = \int_{a}^{b}f(x)\,dx \pm \int_{a}^{b}g(x)\,dx\]
Vertauschungsregel:
\[\int_{a}^{b}f(x)\,dx = -\int_{b}^{a}f(x)\,dx\]
Zerlegung in Teilintervalle:
\(\displaystyle \int_{a}^{b}f(x)\,dx = \int_{a}^{c}f(x)\,dx + \int_{c}^{b}f(x)\,dx\) mit \(a \leq c \leq b\)
\[\begin{align*} A &= \int_{0}^{5}7e^{-0{,}2x}dx \\[0.8em] &= \big[ \underbrace{-35 \cdot e^{-0{,}2x}}_{\text{Stammfunktion}} \big]_{\textcolor{#89ba17}{0}}^{\textcolor{#e9b509}{5}} \\[0.8em] &= -35 \cdot e^{-0{,}2 \cdot \textcolor{#e9b509}{5}} - \big( -35 \cdot \underbrace{e^{-0{,}2 \cdot \textcolor{#89ba17}{0}}}_{1} \big) \\[0.8em] &= -35 \cdot e^{-1} + 35 &&|\; a^{-n} = \frac{1}{a^{n}} \\[0.8em] &= 35 - \frac{35}{e} \\[0.8em] &= 35 \cdot \left( 1 - \frac{1}{e} \right) \\[0.8em] &= 35 \cdot \frac{e - 1}{e} \\[0.8em] &\approx 22{,}12 \end{align*}\]
Prozentualer Anteil des zu \(s = 5\) gehörigen Rechtecks
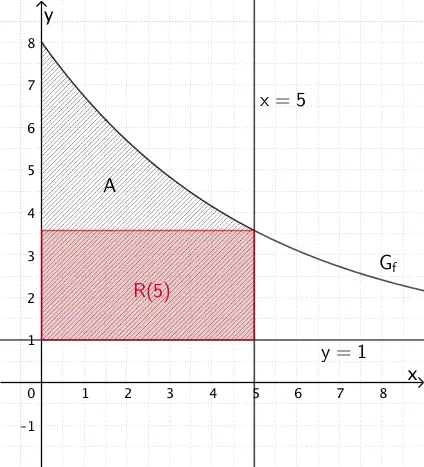
Anteil des Rechtecks mit dem Flächeninhalt \(R(5)\) für \(s = 5\) (vgl. Teilaufgabe 1b)
\(R(s) = 7s \cdot e^{-0{,}2s}\); \(s = 5\) (vgl. Teilaufgabe 1b)
\[R(5) = 7 \cdot 5 \cdot e^{-0{,}2 \cdot 5} = 35 \cdot e^{-1} = 35 \cdot \frac{1}{e}\]
Prozentualen Anteil von \(R(5)\) berechnen:
\[\frac{R(5)}{A} = \frac{\cancel{35} \cdot \frac{1}{\cancel{e}}}{\cancel{35} \cdot \frac{e - 1}{\cancel{e}}} = \frac{1}{e - 1} \approx 0{,}582 = 58{,}2\,\%\]


