Die Abbildung 1 zeigt modellhaft eine Mehrzweckhalle, die auf einer horizontalen Fläche steht und die Form eines geraden Prismas hat.
Die Punkte \(A_{1}(0|0|0)\), \(A_{2}(20|0|0)\), \(A_{3}\) und \(A_{4}(0|10|0)\) stellen im Modell die Eckpunkte der Grundfläche der Mehrzweckhalle dar, die Punkte \(B_{1}\), \(B_{2}\), \(B_{3}\) und \(B_{4}\) die Eckpunkte der Dachfläche. Diejenige Seitenwand, die im Modell in der \(x_{1}x_{3}\)-Ebene liegt, ist 6 m hoch, die ihr gegenüberliegende Wand nur 4 m.
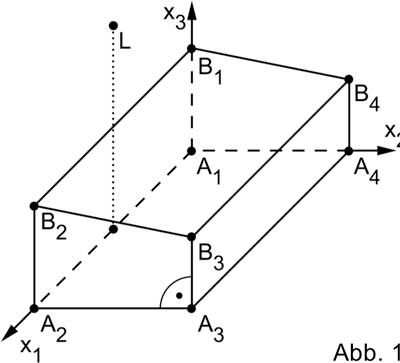
Eine Längeneinheit im Koordinatensystem entspricht 1 m, d.h. die Mehrzweckhalle ist 20 m lang.
Geben Sie die Koordinaten der Punkte \(B_{2}\), \(B_{3}\) und \(B_{4}\) an und bestätigen Sie, dass diese Punkte in der Ebene \(E \colon x_{2} + 5x_{3} - 30 = 0\) liegen.
(4 BE)
Lösung zu Teilaufgabe a
Koordinaten der Punkte \(B_{2}\), \(B_{3}\) und \(B_{4}\)
\(B_{2}(20|0|6)\), \(B_{3}(20|10|4)\), \(B_{4}(0|10|4)\)
Begründung (nicht verlangt)

Der Punkt \(B_{2}\) liegt im Modell 6 LE (vgl. Angabe) vertikal über \(A_{2}(20|0|0)\).
\[\Longrightarrow \quad B_{2}(20|0|6)\]
Der Punkt \(B_{3}\) liegt im Modell 4 LE (vgl. Angabe) vertikal über \(A_{3}\). Da die Mehrzweckhalle im Modell die Form eines geraden Prismas hat, ist die Seitenfläche \(A_{1}A_{2}A_{3}A_{4}\) des Prismas ein Rechteck. Der Punkt \(A_{3}\) hat deshalb die gleiche \(x_{1}\)-Koordinate wie der Punkt \(A_{2}(20|0|0)\) und die gleiche \(x_{2}\)-Koordinate wie der Punkt \(A_{4}(0|10|0)\).
\[\Longrightarrow \quad A_{3}(20|10|0) \quad \Longrightarrow \quad B_{3}(20|10|4)\]
Der Punkt \(B_{4}\) liegt im Modell 4 LE (vgl. Angabe) vertikal über \(A_{4}(0|10|0)\).
\[\Longrightarrow \quad B_{4}(0|10|4)\]
Nachweis, dass die Punkte \(B_{2}\), \(B_{3}\) und \(B_{4}\) in der Ebene \(E\) liegen
\[E \colon x_{2} + 5x_{3} - 30 = 0\]
Der Nachweis erfolgt mithilfe einer Punktprobe.
\(B_{2}(20|\textcolor{#e9b509}{0}|\textcolor{#e9b509}{6}) \;\text{in}\; E\colon \textcolor{#e9b509}{0} + 5 \cdot \textcolor{#e9b509}{6} - 30 = 0 \enspace \textcolor{#89ba17}{\text{(w)}} \enspace\Rightarrow \enspace \textcolor{#89ba17}{B_{2} \in E}\)
\(B_{3}(20|\textcolor{#e9b509}{10}|\textcolor{#e9b509}{4}) \;\text{in} \; E\colon \textcolor{#e9b509}{10} + 5 \cdot \textcolor{#e9b509}{4} - 30 = 0 \enspace \textcolor{#89ba17}{\text{(w)}} \enspace \Rightarrow \enspace \textcolor{#89ba17}{B_{3} \in E}\)
\(B_{4}(0|\textcolor{#e9b509}{10}|\textcolor{#e9b509}{4}) \; \text{in} \; E\colon \textcolor{#e0b509}{10} + 5 \cdot \textcolor{#e9b509}{4} - 30 = 0 \enspace \textcolor{#89ba17}{\text{(w)}} \enspace \Rightarrow \enspace \textcolor{#89ba17}{B_{4} \in E}\)

