Gegeben sind in einem kartesischen Koordinatensystem die Ebene \(E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0\) und die Gerade \(g \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}, \; \lambda \in \mathbb R\,.\)
Erläutern Sie, warum die folgende Rechnung ein Nachweis dafür ist, dass \(g\) und \(E\) genau einen gemeinsamen Punkt haben:
\[\begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix} \circ \begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix} = -72 \neq 0\]
(1 BE)
Lösung zu Teilaufgabe a
\[E \colon 4x_{1} - 8x_{2} + x_{3} + 50 = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{\overrightarrow{n}_{E} = \begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}}\]
Ebenengleichung in Normalenform (vgl. Merkhilfe)
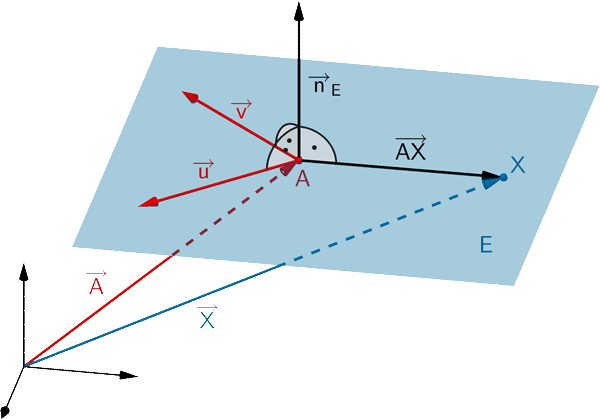
Jeden Ebene lässt sich durch eine Gleichung in Normalenform beschreiben. Ist \(A\) ein beliebiger Aufpunkt der Ebene \(E\) und \(\overrightarrow{n}_{E}\) ein Normalenvektor von \(E\), so erfüllt jeder Punkt \(X\) der Ebene \(E\) folgende Gleichungen:
Normalenform in Vektordarstellung
\[E \colon \overrightarrow{n}_{E} \circ (\overrightarrow{X} - \overrightarrow{A}) = 0\]
Normalenform in Koordinatendarstellung
\[E \colon n_{1}x_{1} + n_{2}x_{2} + n_{3}x_{3} + n_{0} = 0\]
mit \(n_{0} = -(\overrightarrow{n}_{E} \circ \overrightarrow{A}) = - \: n_{1}a_{1} - n_{2}a_{2} - n_{3}a_{3}\)
\(n_{1}\), \(n_{2}\) und \(n_{3}\): Koordinaten eines Normalenvektors \(\overrightarrow{n}_{E}\)
\[g \colon \overrightarrow{X} = \begin{pmatrix} 3 \\ 12 \\ -2 \end{pmatrix} + \lambda \cdot \textcolor{#e9b509}{\begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}}, \; \lambda \in \mathbb R\]
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\textcolor{#0087c1}{\begin{pmatrix} 4 \\ -8 \\ 1 \end{pmatrix}} \textcolor{#cc071e}{\circ} \textcolor{#e9b509}{\begin{pmatrix} 5 \\ 11 \\ -4 \end{pmatrix}} = -72 \textcolor{#cc071e}{\neq 0}\]
Anwendung des Skalarprodukts:
Orthogonale (zueinander senkrechte) Vektoren (vgl. Merkhilfe)
\[\overrightarrow{a} \perp \overrightarrow{b} \quad \Longleftrightarrow \quad \overrightarrow{a} \circ \overrightarrow{b} \quad (\overrightarrow{a} \neq \overrightarrow{0},\; \overrightarrow{b} \neq \overrightarrow{0})\]
Die Gleichung sagt aus, dass das Skalarprodukt aus dem Normalenvektor der Ebenengleichung von \(E\) und dem Richtungsvektor der Geradengleichung von \(g\) ungleich Null ist. Folglich sind der Normalenvektor und der Richtungsvektor nicht zueinander senkrecht. Die Gerade \(g\) verläuft daher nicht parallel zur Ebene \(E\), sondern schneidet die Ebene in genau einem Punkt.

