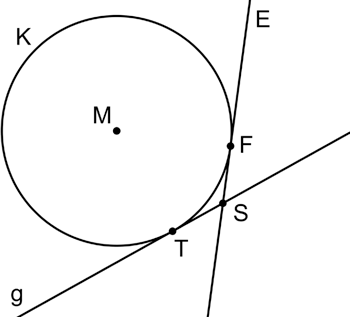
Die Punkte \(M\), \(T\), \(S\) und \(F\) (vgl. die Aufgaben b, c und d) liegen in einer Ebene \(Z\). Die nicht maßstabsgetreue Abbildung zeigt die Gerade \(g\), den Schnitt der Ebene \(E\) mit der Ebene \(Z\) sowie den Schnitt der Kugel \(K\) mit der Ebene \(Z\).
Begründen Sie, dass das Viereck \(MTSF\) einen Umkreis besitzt. Berechnen Sie den Flächeninhalt dieses Vierecks.
(4 BE)
Lösung zu Teilaufgabe e
Begründung, dass das Viereck \(MTSF\) einen Umkreis besitzt
![Punkte F und T auf Thaleskreis über [MS], Umkreis des Vierecks MTSF](/images/stories/B2020_PT_B_G2/B2020_PT_B_G2_e.png)
Die Punkte \(F\) und \(T\) sind Berührpunkte der Ebene \(E\) bzw. der Gerade \(g\) mit der Kugel \(K\). Deshalb sind die Dreiecke \(MSF\) und \(MTS\) bei \(F\) bzw. \(T\) rechtwinklig.
Satz des Thales
Liegt der Punkt \(C\) eines Dreiecks \(ABC\) auf einem Kreis mit dem Durchmesser \([AB]\), ist der Winkel bei Punkt \(C\) ein rechter Winkel.
Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse.
Die Berührpunkte \(F\) und \(T\) liegen auf einem Thaleskreis über dem Durchmesser \([MS]\). Das Viereck \(MTSF\) hat somit einen Umkreis.
Berechnung des Flächeninhalts des Vierecks \(MTSF\)
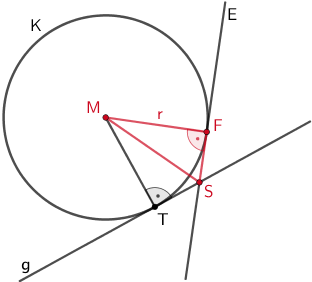
Der Flächeninhalt des Vierecks \(MTSF\) ist doppelt so groß wie der Flächeninhalt des rechtwinkligen Dreiecks \(MSF\) mit den Katheten \([MF]\) und \([FS]\).
\[\begin{align*}A_{MTSF} &= 2 \cdot \textcolor{#cc071e}{A_{MSF}} \\[0.8em] &= 2 \cdot \frac{1}{2} \cdot \textcolor{#cc071e}{\overline{MF}} \cdot \textcolor{#cc071e}{\overline{FS}} &&| \; \textcolor{#cc071e}{\overline{MF} = r} \\[0.8em] &= r \cdot \overline{FS} \end{align*}\]
Länge der Kathete \([FS]\) berechnen:
\(F(-5|4|2)\), \(S(0{,}5|6{,}5|0)\) (vgl. Teilaufgaben b,c)
\[\begin{align*}\overline{FS} &= \vert \overrightarrow{FS} \vert = \vert \overrightarrow{S} - \overrightarrow{F} \vert \\[0.8em] &= \left| \begin{pmatrix} 0{,}5 \\ 6{,}5 \\ 0 \end{pmatrix} - \begin{pmatrix} -5 \\ 4 \\ 2 \end{pmatrix} \right| = \left| \begin{pmatrix} 5{,}5 \\ 2{,}5 \\ -2 \end{pmatrix} \right| \\[0.8em] &= \sqrt{5{,}5^{2} + 2{,}5^{2} + (-2)^{2}} = \sqrt{40{,}5}\end{align*}\]
Mit \(r = 18\) (vgl. Teilaufgabe c) ergibt sich:
\[A_{MTSF} = r \cdot \overline{FS} = 18 \cdot \sqrt{40{,}5} \approx 114{,}55\]
Der Flächeninhalt des Vierecks \(MTSF\) beträgt ungefähr 114,55 FE (Flächeneinheiten).

