Die Abbildung zeigt den Graphen \(G_{f}\) einer in \(\mathbb R\) definierten Funktion \(f\). \(G_{f}\) ist streng monoton fallend und schneidet die \(x\)-Achse im Punkt \((1|0)\).
Betrachtet wird ferner die Funktion \(g\) mit \(g(x) = \dfrac{1}{f(x)}\) und maximalem Definitionsbereich \(D_{g}\).
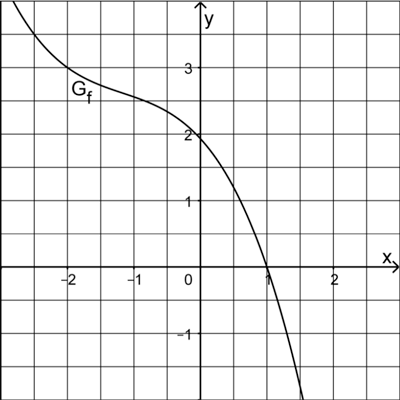
Begründen Sie, dass \(x = 1\) nicht in \(D_{g}\) enthalten ist, und geben Sie den Funktionswert \(g(-2)\) an.
(2 BE)
Lösung zu Teilaufgabe 4a
\[g(x) = \frac{1}{f(x)}\]
Begründung, dass \(x = 1\) nicht in \(D_{g}\) enthalten ist
Da \(G_{f}\) die \(x\)-Achse im Punkt \((\textcolor{#e9b509}{1}|\textcolor{#e9b509}{0})\) schneidet (vgl. Angabe), gilt \(f(\textcolor{#e9b509}{1}) = \textcolor{#e9b509}{0}\). Weil sich somit für \(x = 1\) im Nenner von \(g(x) = \dfrac{1}{f(x)}\) der Wert 0 ergibt, ist \(x = 1\) nicht in \(D_{g}\) enthalten.
Funktionswert \(g(-2)\)
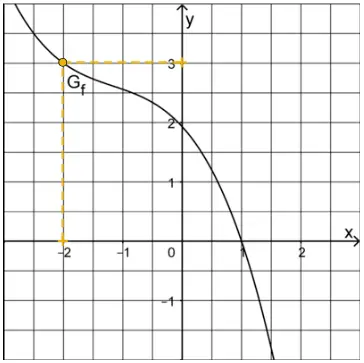
Im Rahmen der Ablesegenauigkeit entnimmt man der Abbildung \(f(\textcolor{#e9b509}{-2}) \approx \textcolor{#e9b509}{3}\).
\[g(\textcolor{#e9b509}{-2}) = \frac{1}{f(\textcolor{#e9b509}{-2})} \approx \frac{1}{\textcolor{#e9b509}{3}}\]

