Die Funktion \(p\) besitzt im Intervall \([4;12]\) eine Wendestelle. Geben Sie die Bedeutung dieser Wendestelle im Sachzusammenhang an.
(2 BE)
Lösung zu Teilaufgabe 3c
Die Wendestelle von \(p\) im Intervall \([4;12]\) entspricht dem Zeitpunkt, zu dem die Leistung der Photovoltaikanlage am stärksten zunimmt.
oder
Die Wendestelle von \(p\) im Intervall \([4;12]\) entspricht dem Zeitpunkt, zu dem die Zunahme der Leistung der Photovoltaikanlage am größten ist.
Ausführliche Erklärung (nicht verlangt)
An den Wendestellen einer Funktion ist die Steigung der Tangente (Wendetangente) an den Graphen der Funktion extremal (am größten oder am kleinsten).
![Wendestelle des Graphen der Funktion p im Intervall [4;12], Wendetangente w](/images/stories/B2021_PT_B_A1/B2021_PT_B_A1_3c.png)
Da der Graph der Funktion \(p\) im Intervall \([4;12]\) (streng monoton) steigt, ist die Steigung der Tangente an der Wendestelle \(x_{w} \in [4;12]\) (Wendetangente \(\textcolor{#cc071e}{w}\)) maximal.
Anwendung der Differetialrechnung:
Steigung \(m_{T}\) einer Tangente \(T\) an den Graphen einer Funktion \(f\) im Punkt \(P\,(\,x_0\,|\,f(x_0)\,)\)
\[m_{T} = f'(x_0)\]
(vgl. Merkhilfe)
Das bedeutet, dass die momentane Änderungsrate \(p'\) der Funktion \(p\) an der Wendestelle \(x_{w} \in [4;12]\) ein Maximum erreicht.
Differentialquotient oder lokale bzw. momentane Änderungsrate
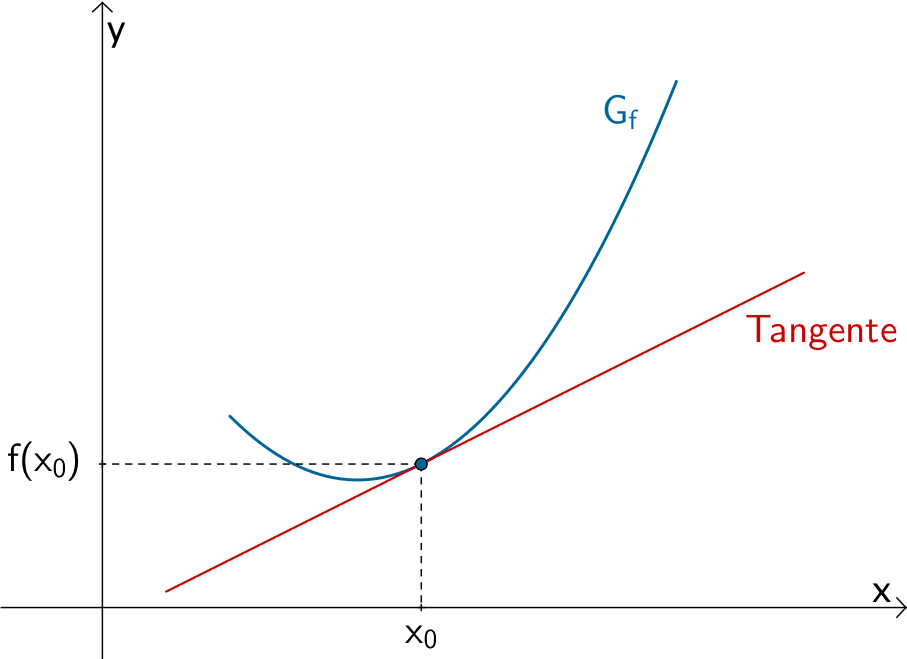
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Im Sachzusammenhang beschreibt die momentane Änderungsrate von \(p\) die Änderung der Leistung der Photovoltaikanlage pro Zeiteinheit zu einem betrachteten Zeitpunkt.
Zum Zeitpunkt \(x_{w} \in [4;12]\) ist die Änderung der Leistung der Anlage in kW/h (Kilowatt pro Stunde) maximal. Oder anders formuliert: Die Zunahme der Leistung ist zum Zeitpunkt \(x_{w}\) am größten.


