Betrachtet wird nun die Schar der in \(\mathbb R\) definierten Funktionen \(h_{k} \colon x \mapsto (1 - kx^{2}) \cdot e^{-x}\) mit \(k \in \mathbb R\). Der Graph von \(h_{k}\) wird mit \(G_{k}\) bezeichnet. Für \(k = 1\) ergibt sich die bisher betrachtetet Funktion \(f\).
Geben Sie in Abhängigkeit von \(k\) die Anzahl der Nullstellen von \(h_{k}\) an.
(2 BE)
Lösung zu Teilaufgabe 1g
\[h_{k}(x) = (1 - kx^{2}) \cdot e^{-x}; \; k \in \mathbb R, \; D_{h_{k}} = \mathbb R\]
\(k \leq 0\): keine Nullstelle
\(k > 0\): zwei Nullstellen
Begründung (nicht verlangt)
\[h_{k}(x) = (1 - kx^{2}) \cdot \textcolor{#e9b509}{\underbrace{e^{-x}}_{>\,0}}; \; k \in \mathbb R, \; D_{h_{k}} = \mathbb R\]
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).

Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
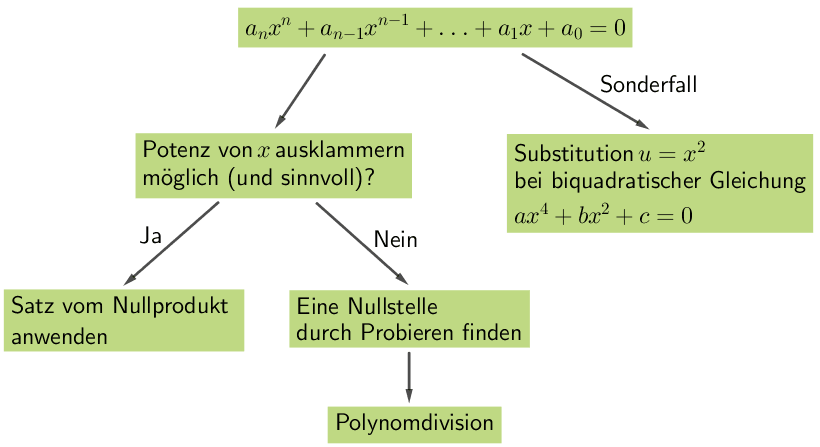
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
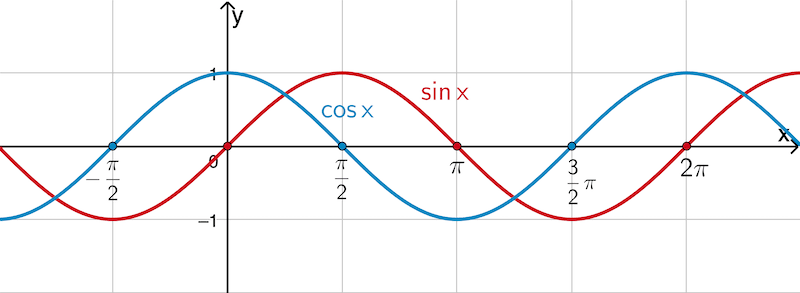
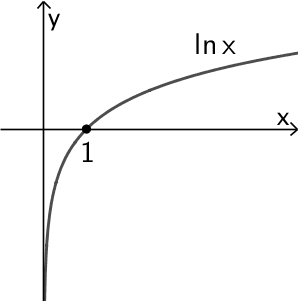
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
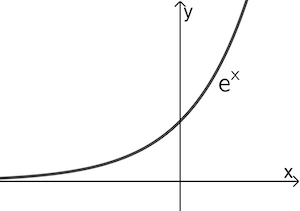
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
 (Skizze nicht verlangt)
(Skizze nicht verlangt)
Da der Wert des Exponetialterms \(\textcolor{#e9b509}{e^{-x}}\) für alle \(x \in \mathbb R\) stets größer als null ist, folgt:
\[h_{k}(x) = 0 \enspace \Rightarrow \enspace 1 - kx^{2} = 0\]
Für \(k \textcolor{#cc071e}{<} 0\) folgt \(1 - \textcolor{#cc071e}{\underbrace{kx^{2}}_{<\,0}} > 0\) und
für \(k = 0\) folgt \(1 \neq 0\).
Somit hat \(h_{k}\) für \(k \leq 0\) keine Nullstelle.
Für \(k > 0\) ergibt sich:
\[\begin{align*}1 - kx^{2} &= 0 &&| + kx^{2} \\[0.8em] 1 &= kx^{2} &&| : k \\[0.8em] \frac{1}{k} &= x^{2} &&| \; \sqrt{\quad} \\[0.8em] \pm\sqrt{\frac{1}{k}} &= x_{1,2}\end{align*}\]
Somit hat \(h_{k}\) für \(k > 0\) zwei Nullstellen.

