Auf der Strecke \([DE]\) gibt es einen Punkt \(K\), für den \(\overline{KE} = \overline{EF}\) gilt.
Bestimmen Sie die Koordinaten von \(K\).
(4 BE)
Lösung zu Teilaufgabe d
1. Möglichkeit: Einheitsvektor \(\overrightarrow{ED}^{\circ}\)
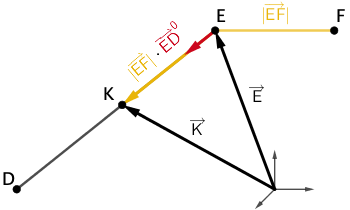
Planskizze (optional): Der Einheitsvektor \(\textcolor{#cc071e}{\overrightarrow{ED}^{0}}\) hat die Länge 1. Es gilt: \(\overrightarrow{EK} = \textcolor{#cc071e}{\overrightarrow{ED}^{0}} \cdot \textcolor{#e9b509}{\vert \overrightarrow{EF}\vert}\).
Durch Vektoraddition ergibt sich:
\[\begin{align*} \overrightarrow{K} &= \overrightarrow{E} + \overrightarrow{EK} \\[0.8em] &= \overrightarrow{E} +\textcolor{#e9b509}{\vert \overrightarrow{EF}\vert} \cdot \textcolor{#cc071e}{\overrightarrow{ED}^{0}}\end{align*}\]
Länge der Verbindungsvektoren \(\overrightarrow{ED}\) und \(\textcolor{#e9b509}{\overrightarrow{EF}}\) berechnen:
\(D(5|-5|0)\), \(E(2|0|4)\), \(F(0|2|4)\)
\[\begin{align*}\vert\overrightarrow{ED}\vert &= \vert \overrightarrow{D} - \overrightarrow{E}\vert \\[0.8em] &= \left| \begin{pmatrix} 5 \\ -5 \\ 0 \end{pmatrix} - \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} \right| = \left| \begin{pmatrix} 3 \\ -5 \\ -4 \end{pmatrix} \right| \\[0.8em] &= \sqrt{3^{2} + (-5)^{2} + (-4)^{2}} = \sqrt{50} = 5\sqrt{2}\end{align*}\]
\[\begin{align*}\textcolor{#e9b509}{\vert\overrightarrow{EF}\vert} &= \vert \overrightarrow{F} - \overrightarrow{E}\vert \\[0.8em] &= \left| \begin{pmatrix} 0 \\ 2 \\ 4 \end{pmatrix} - \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} \right| = \left| \begin{pmatrix} -2 \\ 2 \\ 0 \end{pmatrix} \right| \\[0.8em] &= \sqrt{2^{2} + 2^{2} + 0^{2}} = \sqrt{8} = \textcolor{#e9b509}{2\sqrt{2}}\end{align*}\]
Einheitsvektor \(\textcolor{#cc071e}{\overrightarrow{ED}^{\circ}}\) berechnen:
Einheitsvektor (vgl. Merkhilfe)
\[\overrightarrow{a}^0 = \frac{\overrightarrow{a}}{\vert \overrightarrow{a} \vert}\]
Vektoren mit der Länge 1 heißen Einheitsvektoren.
\[\textcolor{#cc071e}{\overrightarrow{ED}^{\circ}} = \frac{\overrightarrow{ED}}{\vert \overrightarrow{ED} \vert} = \frac{\begin{pmatrix} 3 \\ -5 \\ -4 \end{pmatrix}}{5\sqrt{2}} = \textcolor{#cc071e}{\frac{1}{5\sqrt{2}} \cdot \begin{pmatrix} 3 \\ -5 \\ -4 \end{pmatrix}}\]
Koordinaten von \(K\) bestimmen:
\[\begin{align*} \overrightarrow{K} &= \overrightarrow{E} +\textcolor{#e9b509}{\vert \overrightarrow{EF}\vert} \cdot \textcolor{#cc071e}{\overrightarrow{ED}^{0}}\\[0.8em] &= \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} + \textcolor{#e9b509}{2\cancel{\sqrt{2}}} \cdot \textcolor{#cc071e}{\frac{1}{5\cancel{\sqrt{2}}} \cdot \begin{pmatrix} 3 \\ -5 \\ -4 \end{pmatrix}} \\[0.8em] &=\begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} + 0{,}4 \cdot \begin{pmatrix} 3 \\ -5 \\ -4 \end{pmatrix} \\[0.8em] &= \begin{pmatrix} 3{,}2 \\ -2 \\ 2,4 \end{pmatrix} \enspace \Rightarrow \enspace K(3{,}2|-2|2{,}4) \end{align*}\]
2. Möglichkeit: Punkt \(K\) als Punkt der Strecke \([DE]\) beschreiben
Dieser Lösungsansatz ist deutlich rechenintensiver.
\(D(5|-5|0)\), \(E(2|0|4)\)
Strecke \([DE]\) in Parameterform beschreiben:
\[\overrightarrow{DE}=\overrightarrow{E} - \overrightarrow{D}= \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 5 \\ -5 \\ 0 \end{pmatrix} = \begin{pmatrix} -3 \\ 5 \\ 4 \end{pmatrix}\]
Gleichung einer Gerad / Strecke in Parameterform
Jede Gerade \(g\) kann durch eine Gleichung in der sogenannten Parameterform
\(g \colon \overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{u} \enspace\) mit dem Parameter \(\lambda \in \mathbb R\) beschrieben werden.
Dabei ist \(\overrightarrow{A}\) der Ortsvektor eines Aufpunkts (Stützvektor) und \(\overrightarrow{u}\) ein Richtungsvektor der Gerade \(g\).
Gleichung einer Strecke \([AB]\) in Parameterform:
\[\overrightarrow{X} = \overrightarrow{A} + \lambda \cdot \overrightarrow{AB}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \]
\[\begin{align*} [DE]\colon \overrightarrow{X} &= \overrightarrow{D} + \textcolor{#cc071e}{\lambda} \cdot \overrightarrow{DE}, \; \textcolor{#cc071e}{\lambda \in [0;1]} \\[0.8em] [DE]\colon \overrightarrow{X} &= \begin{pmatrix}5\\-5\\0 \end{pmatrix} + \textcolor{#cc071e}{\lambda} \cdot \begin{pmatrix} -3\\5\\4 \end{pmatrix}, \;\textcolor{#cc071e}{\lambda \in [0;1]}\end{align*}\]
Der Punkt \(K\) liegt auf der Strecke \([DE]\). Somit folgt:
\[K \in [DE]\colon \overrightarrow{K} = \begin{pmatrix} 5 - 3\textcolor{#cc071e}{\lambda}\\-5 + 5\textcolor{#cc071e}{\lambda}\\4\textcolor{#cc071e}{\lambda} \end{pmatrix}, \;\textcolor{#cc071e}{\lambda \in [0;1]}\]
Koordinaten des Punktes \(K\) ermitteln, für den \(\overline{KE} = \overline{EF}\) gilt:
\(E(2|0|4)\), \(F(0|2|4)\)
Betrag eines Vektors
\[ \vert \overrightarrow{a} \vert = \sqrt{\overrightarrow{a} \circ \overrightarrow{a}} = \sqrt{{a_1}^2 + {a_2}^2 + {a_3}^2}\]
(vgl. Merkhilfe)
\[\begin{align*}\overline{KE} &= \overline{EF} \\[0.8em] \vert \overrightarrow{KE} \vert &= \vert\overrightarrow{EF}\vert \\[0.8em] \vert \overrightarrow{E} - \overrightarrow{K} \vert &= \vert \overrightarrow{F} - \overrightarrow{E} \vert \\[0.8em] \left| \begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} - \begin{pmatrix} 5 - 3\textcolor{#cc071e}{\lambda}\\-5 + 5\textcolor{#cc071e}{\lambda}\\4\textcolor{#cc071e}{\lambda} \end{pmatrix} \right| &= \left| \begin{pmatrix} 0 \\ 2 \\ 4 \end{pmatrix}-\begin{pmatrix} 2 \\ 0 \\ 4 \end{pmatrix} \right| \\[0.8em] \left| \begin{pmatrix} -3 + 3\lambda \\ 5 - 5\lambda \\4 - 4\lambda \end{pmatrix}\right| &= \left| \begin{pmatrix} -2 \\ 2 \\ 0 \end{pmatrix}\right| \\[0.8em] \sqrt{(-3 + 3\lambda)^{2} + (5 - 5\lambda)^{2} + (4 - 4\lambda)^{2}} &= \sqrt{(-2)^{2} + 2^{2} + 0^{2}} &&| \;(\dots)^{2}\;\text{(Quadrieren)} \\[0.8em] 9 - 18\lambda + 9\lambda^{2} + 25 - 50\lambda +25\lambda^{2} + 16 - 32\lambda + 16\lambda^{2} &= 8 \\[0.8em] 50\lambda^{2} - 100\lambda + 50 &= 8 &&| - 8 \\[0.8em] 50\lambda^{2} - 100\lambda + 42 &= 0\end{align*}\]
Lösungsformel für quadratische Gleichungen (Mitternachtsformel) verwenden:
Lösungsformel für quadratische Gleichungen (vgl. Merkhilfe)
\[ax^2 + bx + c = 0 \,, \qquad a, b, c \in \mathbb R \,, \quad a \neq 0\]
\[\begin{align*} x_{1,2} &= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \quad b^2 \geq 4ac \\[0.8em] x_{1,2} &= \frac{-b \pm \sqrt{D}}{2a}, \quad D \geq 0 \end{align*}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
\[\begin{align*}\lambda_{1,2} &= \frac{100 \pm \sqrt{(-100)^{2} - 4 \cdot 50 \cdot 42}}{2 \cdot 100} &&| \; \textcolor{#cc071e}{\lambda \in [0;1]} \\[0.8em] &= \frac{100 \pm \sqrt{1600}}{100} \\[0.8em] &= \frac{100 \pm 40}{100} \\[0.8em] \Rightarrow \enspace \lambda_{1} &= \frac{100 - 40}{100} = \frac{60}{100} = 0{,}6 \\[0.8em] \bigg( \lambda_{2} &= \frac{100 + 40}{100} = \frac{140}{100} = 1{,}4 \textcolor{#cc071e}{\not \in [0;1]} \bigg) \end{align*}\]
Mit \(\textcolor{#cc071e}{\lambda = 0{,}6}\) ergibt sich:
\[\begin{align*}\overrightarrow{K} &= \begin{pmatrix} 5 - 3\textcolor{#cc071e}{\lambda}\\-5 + 5\textcolor{#cc071e}{\lambda}\\4\textcolor{#cc071e}{\lambda} \end{pmatrix} = \begin{pmatrix} 5 - 3 \cdot \textcolor{#cc071e}{0{,}6}\\-5 + 5 \cdot\textcolor{#cc071e}{0{,}6}\\4 \cdot \textcolor{#cc071e}{0{,}6} \end{pmatrix} = \begin{pmatrix} 3{,}2 \\ -2 \\ 2{,}4 \end{pmatrix}\\[0.8em] &\Rightarrow \enspace K(3{,}2|-2|2{,}4)\end{align*}\]

