Teilaufgabe 2a

Lösung zu Teilaufgabe 2a

1.Lösungsansatz: Baumdiagramm (2-stufiges Zufallsexperiment)

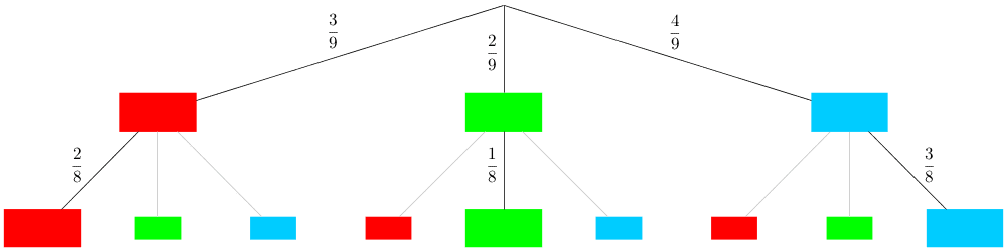
Die Kiste enthält insgesamt \(4 + 2 + 3 = 9\) Bausteine.

Betrachtet werden die Ereignisse \(\{R,R\}\) (zweimal Rot), \(\{G,G\}\) (zweimal Grün) und \(\{B,B\}\) (zweimal Blau).

Entnehmen von zwei Bausteinen gleicher Farbe:

\[P(\{R,R\}) = \frac{3}{9} \cdot \frac{2}{8} = \frac{6}{72} = \frac{3}{36}\]

\[P(\{G,G\}) = \frac{2}{9} \cdot \frac{1}{8} = \frac{2}{72} = \frac{1}{36}\]

\[P(\{B,B\}) = \frac{4}{9} \cdot \frac{3}{8} = \frac{12}{72} = \frac{6}{36}\]

\[\begin{align*}P(\text{gleiche Farbe}) &= P(\{R,R\}) + P(\{G,G\}) + P(\{B,B\}) \\[0.8em] &= \frac{3}{36} + \frac{1}{36} + \frac{6}{36} \\[0.8em] &= \frac{10}{36} = \frac{5}{18}\end{align*}\]

2. Lösungsansatz: Ziehen mit einem Griff (1-stufiges Zufallsexperiment)

Da die Reihenfolge der entnommenen Bausteine keine Rolle spielt, macht es keinen Unterschied, ob diese nacheinander einzeln ohne Zurücklegen oder beide zusammen mit einem Griff entnommen werden werden.

Die Kiste enthält insgesamt \(4 + 2 + 3 = 9\) Bausteine.

Betrachtet werden die Ereignisse \(\{R,R\}\) (zweimal Rot), \(\{G,G\}\) (zweimal Grün) und \(\{B,B\}\) (zweimal Blau).

\[\begin{align*}P(\text{gleiche Farbe}) &= P(\{R,R\}) + P(\{G,G\}) + P(\{B,B\}) \\[0.8em] &= \frac{\displaystyle \binom{4}{2} \cdot \binom{5}{0}}{\displaystyle \binom{9}{2}} + \frac{\displaystyle \binom{2}{2} \cdot \binom{7}{0}}{\displaystyle \binom{9}{2}} + \frac{\displaystyle \binom{3}{2} \cdot \binom{6}{0}}{\displaystyle \binom{9}{2}} & &|\; \text{siehe Nebenrechnung} \\[0.8em] &= \frac{6}{36} + \frac{1}{36} + \frac{3}{36} \\[0.8em] &= \frac{10}{36} = \frac{5}{18}\end{align*}\]

Nebenrechnung:

Da der Prüfungsteil A keine Hilfsmittel erlaubt, seien abschließend noch die Berechnungen der Binomialkoeffizienten ohne Taschenrechner aufgeführt. 

\[\binom{4}{2} = \frac{4!}{2! \cdot 2!} = \frac{1 \cdot 2 \cdot 3 \cdot 4}{1 \cdot 2 \cdot 1 \cdot 2} = 6\]

\[\binom{5}{0} = \frac{5!}{0! \cdot 5!} = 1\]

\[\binom{2}{2} = \frac{2!}{2! \cdot 0!} = 1\]

\[\binom{7}{0} = \frac{7!}{0! \cdot 7!} = 1\]

\[\binom{3}{2} = \frac{3!}{2! \cdot 1!} = \frac{1 \cdot 2 \cdot 3}{1 \cdot 2 \cdot 1} = 3\]

\[\binom{6}{0} = \frac{6!}{0! \cdot 6!} = 1\]

\[\binom{9}{2} = \frac{9!}{2! \cdot 7!} = \frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 8 \cdot 9}{1 \cdot 2 \cdot 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 \cdot 7} = \frac{8 \cdot 9}{1 \cdot 2} = \frac{72}{2} = 36\]

Anmerkung:

\[\binom{n}{0} = 1\,; \quad \binom{n}{k = n} = 1\,; \quad \binom{n}{k = n - 1} = n\,;\]