Teilaufgabe b

Stochastik 2

Erstellen Sie zu der beschriebenen Situation ein vollständig beschriftetes Baumdiagramm oder eine vollständig ausgefüllte Vierfeldertafel.

(4 BE) 

Lösung zu Teilaufgabe b

 

Ereignisse:

 

\(A\): „Ein zufällig ausgewählter Angestellter gilt als aufgeschlossen"

\(R\): „Ein zufällig ausgewählter Angestellter hat eine nach rechts geneigte Handschrift"

 

Analyse der Angabe:

 

„In einem Unternehmen mit 50 Angestellten gelten 35 als aufgeschlossen."

\( \Longrightarrow \quad P(A) = \frac {35}{50} = 0{,}7\)

 

„40 % der als aufgeschlossen geltenden Angestellten haben eine Handschrift, die nicht nach rechts geneigt ist."

\(\Longrightarrow \quad P_A(\overline R) = 0{,}4\)

 

„Sechs Angestellte, die nicht als aufgeschlossen gelten, haben eine nach rechts geneigte Handschrift."

\(\Longrightarrow \quad P(\overline A \cap R) = \frac{6}{50} = 0{,}12\)

 

Baumdiagramm

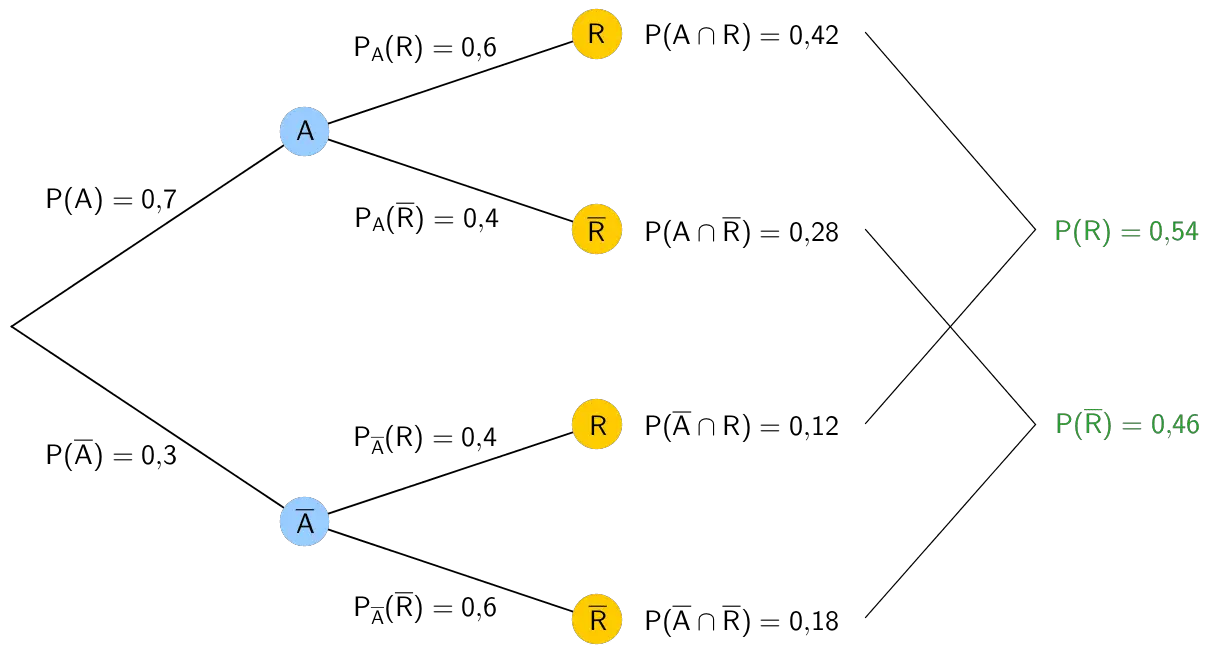
Baumdiagramm, Wahrscheinlichkeiten gemäß Angabe

 

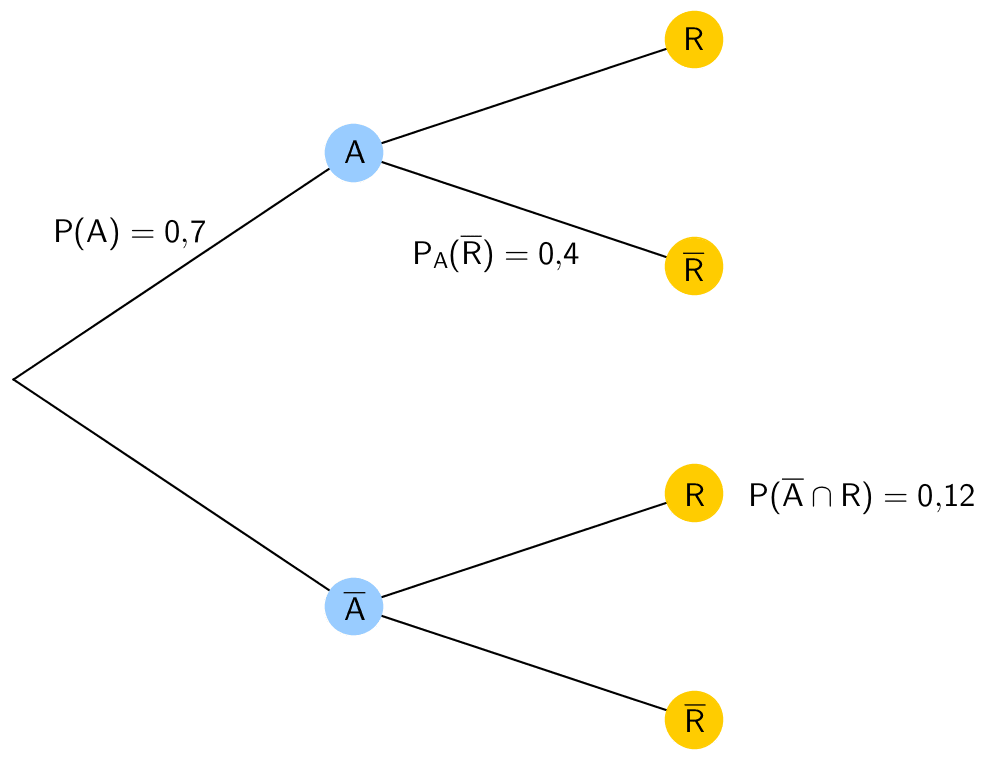
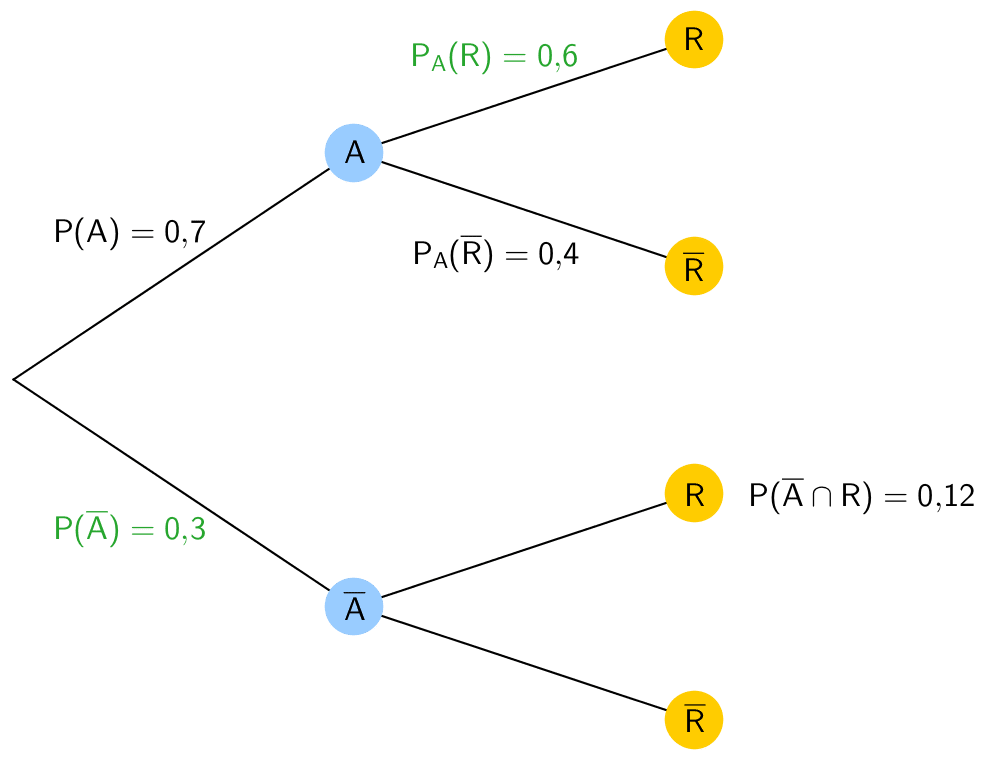
Wahrscheinlichkeiten der Gegenereignisse berechnen (Knotenregel anwenden):

\[P(\overline A) = 1 - P(A) = 1 - 0{,}7 = 0{,}3\]

 

\[P_A(R) = 1 - P_A(\overline R) = 1 - 0{,}4 = 0{,}6\]

 

Baumdiagramm, ergänzt um die Wahrscheinlichkeiten der Gegenereignisse

 

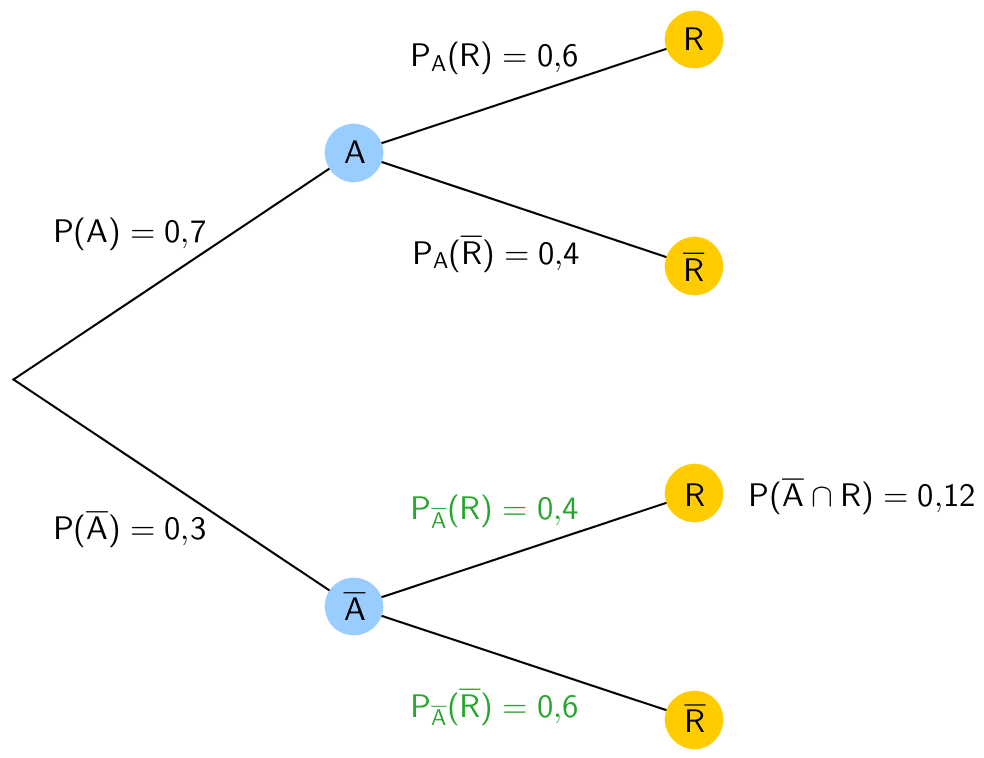
Bedingte Wahrscheinlichkeiten der zweiten Pfade berechnen:

\[P_{\overline A}(R) = \frac{P(\overline A \cap R)}{P(R)} = \frac{0{,}12}{0{,}3} = 0{,}4\]

 

\[P_{\overline A}(\overline R) = 1 - P_{\overline A}(R) = 1 - 0{,}4 = 0{,}6\]

 

Baumdiagramm, ergänzt um die bedingten Wahrscheinlichkeiten der zweiten Pfade

 

Wahrscheinlichkeiten der Schnittmengen berechnen (1. Pfadregel anwenden):

\[P(A \cap R) = P_A(R) \cdot P(A) = 0{,}6 \cdot 0{,}7 = 0{,}42\]

 

\[P(A \cap \overline R) = P_A(\overline R) \cdot P(A) = 0{,}4 \cdot 0{,}7 = 0{,}28\]

 

\[P(\overline A \cap \overline R) = P_{\overline A}(\overline R) \cdot P(\overline A) = 0{,}3 \cdot 0{,}6 = 0{,}18\]

 

Baumdiagramm, ergänzt um die Wahrscheinlichkeiten der Schnittmengen

 

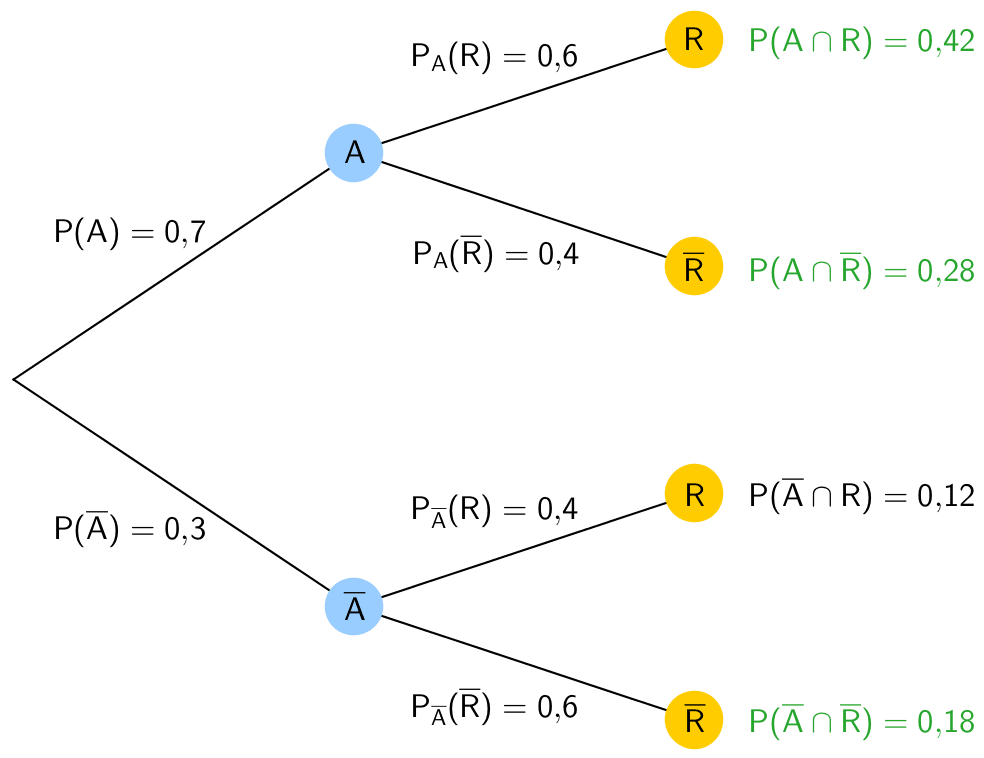
Wahrscheinlichkeiten der Ereignisse \(R\) und \(\overline{R}\) berechnen (2. Pfadregel anwenden):

\[P(R) = P(A \cap R) + P(\overline A \cap R) = 0{,}42 + 0{,}12 = 0{,}54\]

 

\[P(\overline R) = 1 - P(R) = 1 - 0{,}54 = 0{,}46\]

 

Baumdiagramm, ergänzt um die Wahrscheinlichkeiten P(R) und P(nicht R)

 

Vierfeldertafel

 

Gegeben: \(P(A) = \frac {35}{50} = 0{,}7\)

 

\[P(\overline A) = 1 - P(A) = 1 - 0{,}7 = 0{,}3\]

 

  \(R\) \(\overline R\)  
\(A\)     \(P(A) = 0{,}7\)
\(\overline A\)     \(P(\overline A) = 0{,}3\)
      \(1\)

 

Gegeben: \(P(\overline A \cap R) = \frac{6}{50} = 0{,}12\)

 

\[P(\overline A \cap \overline R) = P(\overline A) - P(\overline A \cap R) = 0{,}3 - 0{,}12 = 0{,}18\]

 

  \(R\) \(\overline R\)  
\(A\)     \(P(A) = 0{,}7\)
\(\overline A\) \(P(\overline A \cap R) = 0{,}12\) \(P(\overline A \cap \overline R) = 0{,}18\) \(P(\overline A) = 0{,}3\)
      \(1\)

 

Gegeben: \(P_A(\overline R) = 0{,}4\)

 

\[P_A(\overline R) = \frac{P(A \cap \overline R)}{P(A)} \Longleftrightarrow P(A \cap \overline R) = P_A(\overline R) \cdot P(A) = 0{,}4 \cdot 0{,}7 = 0{,}28\]

 

\[P(A \cap R) = P(A) - P(A \cap \overline R) = 0{,}7 - 0{,}28 = 0{,}42\]

 

\[P(R) = P(A \cap R) + P(\overline A \cap R) = 0{,}42 + 0{,}12 = 0{,}54\]

 

\[P(\overline R) = 1 - P(R) = 1 - 0{,}54 = 0{,}46\]

 

  \(R\) \(\overline R\)  
\(A\) \(P(A \cap R) = 0{,}42\) \(P(A \cap \overline R) = 0{,}28\) \(P(A) = 0{,}7\)
\(\overline A\) \(P(\overline A \cap R) = 0{,}12\) \(P(\overline A \cap \overline R) = 0{,}18\) \(P(\overline A) = 0{,}3\)
  \(P(R) = 0{,}54\) \(P(\overline R) = 0{,}46\) \(1\)
Tags
Weitere Lösungen dieser Aufgabengruppe: « Teilaufgabe a Teilaufgabe c »