Abiturlösungen Mathematik Bayern Beispiel-Abiturprüfung 2014 Prüfungsteil B Analysis 1
- Details
- Kategorie: Analysis 1
Gegeben ist die Funktion \(h\,\colon x \mapsto -\frac{1}{2}x^2 + 2\) mit Definitionsbereich \(\mathbb R\). Der Graph von \(h\) wird mit \(G_h\) bezeichnet.
Geben Sie die Nullstellen von \(h\) an und zeichnen Sie \(G_h\) in ein Koordinatensystem ein.
(3 BE)
- Details
- Kategorie: Analysis 1
Dem Flächenstück, das \(G_h\) mit der \(x\)-Achse vollständig einschließt, werden Rechtecke so einbeschrieben, dass jeweils eine Seite des Rechtecks auf der \(x\)-Achse liegt. Berechnen Sie den größtmöglichen Flächeninhalt \(A\) eines solchen Rechtecks.
(Ergebnis: \(A = \frac{16}{9}\sqrt{3}\))
(6 BE)
- Details
- Kategorie: Analysis 1
Berechnen Sie den Anteil (in Prozent), den das Rechteck mit dem Flächeninhalt \(A\) am Inhalt des Flächenstücks einnimmt, das \(G_h\) mit der \(x\)-Achse vollständig einschließt.
(4 BE)
- Details
- Kategorie: Analysis 1
Gegeben sind die in \(\mathbb R\) definierten Funktionen \(p\,\colon x \mapsto e^{-\frac{1}{4}x}\) und \(q\,\colon x \mapsto e^{-\frac{1}{4}x} \cdot \cos x\). Die Abbildung zeigt den Graphen \(G_q\) von \(q\) füe \(x \geq 0\).
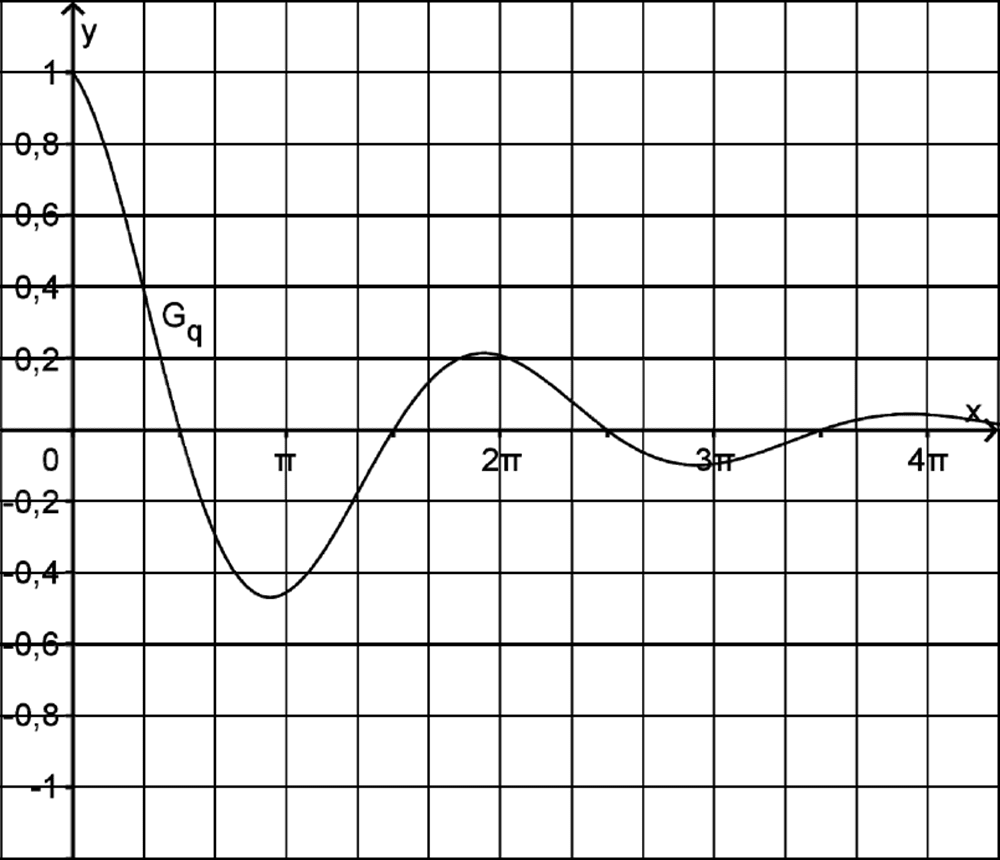
Untersuchen Sie das Monotonieverhalten des Graphen von \(p\) und geben Sie das Verhalten von \(p\) für \(x \to +\infty\) und \(x \to -\infty\) an.
(4 BE)
- Details
- Kategorie: Analysis 1
Berechnen Sie die Funktionswerte \(p(0)\), \(p(\pi)\), \(p(2\pi)\), \(p(3\pi)\) und \(p(4\pi)\). Zeichnen Sie für \(x \geq 0\) den Graphen von \(p\) sowie den Graphen der in \(\mathbb R\) definierten Funktion \(-p\,\colon x \mapsto -p(x)\) unter Berücksichtigung der bisherigen Ereignisse in die Abbildung ein.
(4 BE)
- Details
- Kategorie: Analysis 1
Der Funktionsterm von \(q\) entsteht aus dem Term der in \(\mathbb R\) definierten Kosinusfunktion \(x \mapsto \cos x\) durch Multiplikation mit \(p(x)\). Beschreiben Sie, wie sich der Graph von \(q\) aufgrund dieser Multiplikation vom Graphen der Kosinusfunktion unterscheidet. Gehen Sie dabei auch auf die Nullstellen von \(q\) und die Funktionswerte \(q(n\pi)\) mit \(n \in \mathbb Z\) ein.
(3 BE)
- Details
- Kategorie: Analysis 1
Berechnen Sie den Term \(q'(x)\) der ersten Ableitung von \(q\) und weisen Sie für die Funktion \(q\) nach, dass für die Extremstellen \(\tan x = -0{,}25\) gilt. Zeigen Sie damit, dass die Extremstellen von \(q\) nicht mit den Extremstellen der Kosinusfunktion übereinstimmen.
(6 BE)
- Details
- Kategorie: Analysis 1
Entscheiden Sie, ob die folgenden Aussagen wahr oder falsch sind; machen Sie jeweils Ihre Entscheidung plausibel.
α) \(\lim \limits_{x\,\to\,-\infty} q(x) = +\infty\)
β) \(\lim \limits_{x\,\to\,+\infty} q(x) = 0\)
(4 BE)
- Details
- Kategorie: Analysis 1
Die in \(\mathbb R\) definierte Funktion \(Q\,\colon x \mapsto \frac{16}{17}e^{-\frac{1}{4}x} \cdot \left( \sin x - \frac{1}{4}\cos x \right)\) ist eine Stammfunktion von \(q\).
Zeigen Sie rechnerisch, dass \(\displaystyle \int_0^{2\pi} q(x)\,dx > 0\) gilt, und deuten Sie die Aussage dieser Ungleichung am Graphen von \(q\).
(3 BE)
- Details
- Kategorie: Analysis 1
Es gibt Werte \(a \in \mathbb R^+\), für die \(\displaystyle \int_0^{a} q(x)\,dx < 0\) gilt. Geben Sie einen solchen Wert an und begründen Sie Ihre Antwort ohne zu rechnen.
(3 BE)

