Der Würfel wird entlang der Ebene \(L\) geteilt. Berechnen Sie das Volumen der entstehenden Pyramide. Geben Sie an, wie viel Prozent des Würfelvolumens die Pyramide einnimmt.
(4 BE)
Lösung zu Teilaufgabe b
Volumen der entstehenden Pyramide
1. Lösungsansatz: Elementargeometrischer Ansatz
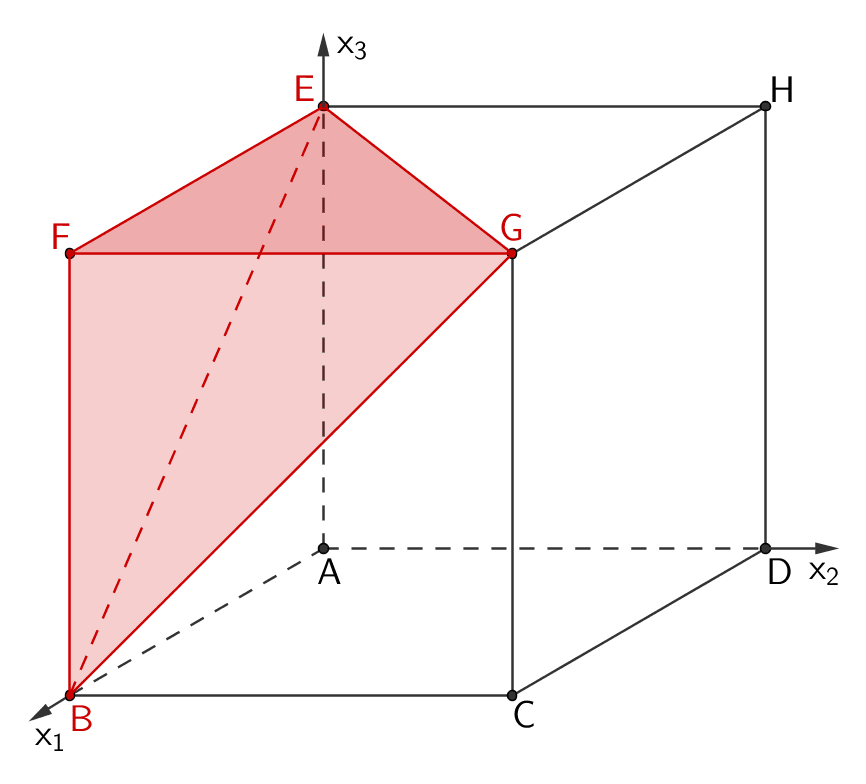
\[V = \frac{1}{3} \cdot G \cdot h\]
\[G = A_{FGE} = \frac{1}{2} \cdot \overline{FG} \cdot \overline{FE} = \frac{1}{2} \cdot 6 \cdot 6 = 18\]
\[h = \overline{FB} = 6\]
\[V_{\text{Pyramide}} = \frac{1}{3} \cdot 18 \cdot 6 = 36\]
2. Lösungsansatz: Anwenden des Spatprodukts
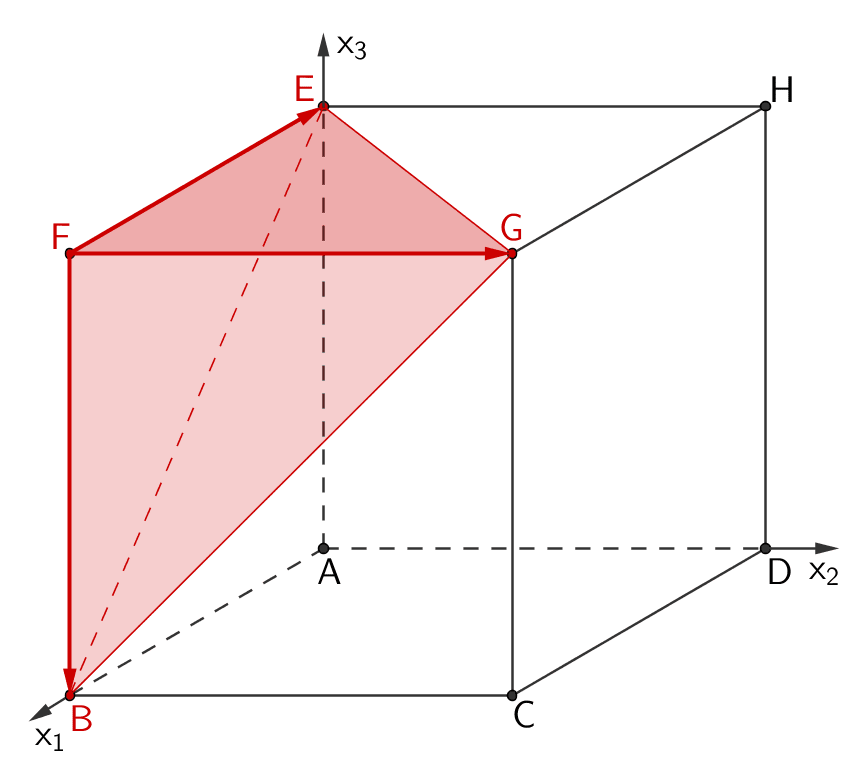
Anwendung des Vekorprodukts - Spatprodukt (vgl. Merkhilfe)
Volumen eines Spats
\[V_{\text{Spat}} = \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
Volumen einer dreiseitigen Pyramide
\[V_{\text{Pyramide}} = \frac{1}{6} \left| \left( \overrightarrow{a} \times \overrightarrow{b} \right) \circ \overrightarrow{c} \; \right|\]
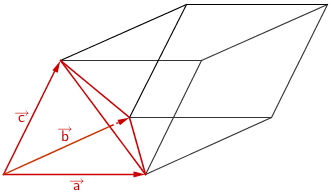
\[V_{\text{Pyramide}} = \frac{1}{6} \cdot \left| \left( \overrightarrow{FE} \times \overrightarrow{FG} \right) \circ \overrightarrow{FB}|\, \right|\]
\[B\,(6|0|0)\,\enspace E\,(0|0|6)\,\enspace F\,(6|0|6)\,\enspace G\,(6|6|6)\]
\[\overline{FE} = \overrightarrow {E} - \overrightarrow {F} = \begin {pmatrix} 0 \\ 0 \\ 6 \end {pmatrix} - \begin {pmatrix} 6 \\ 0 \\ 6 \end {pmatrix} = \begin {pmatrix} -6 \\ 0 \\ 0 \end {pmatrix}\]
\[\overline{FG} = \overrightarrow {G} - \overrightarrow {F} = \begin {pmatrix} 6 \\ 6 \\ 6 \end {pmatrix} - \begin {pmatrix} 6 \\ 0 \\ 6 \end {pmatrix} = \begin {pmatrix} 0 \\ 6 \\ 0 \end {pmatrix}\]
\[\overline{FB} = \overrightarrow {B} - \overrightarrow {F} = \begin {pmatrix} 6 \\ 0 \\ 0 \end {pmatrix} - \begin {pmatrix} 6 \\ 0 \\ 6 \end {pmatrix} = \begin {pmatrix} 0 \\ 0 \\ -6 \end {pmatrix}\]
Vektorprodukt (Kreuzprodukt)
Das Vektorprodukt \(\overrightarrow{a} \times \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) erzeugt einen neuen Vektor \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) mit den Eigenschaften:
\(\overrightarrow{c}\) ist sowohl zu \(\overrightarrow{a}\) als auch zu \(\overrightarrow{b}\) senkrecht.
\[\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b} \quad \Longrightarrow \quad \overrightarrow{c} \perp \overrightarrow{a}, \enspace \overrightarrow{c} \perp \overrightarrow{b}\]
Der Betrag des Vektorprodukts zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) ist gleich dem Produkt aus den Beträgen der Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) und dem Sinus des von ihnen eingeschlossenen Winkels \(\varphi\).
\[\vert \overrightarrow{a} \times \overrightarrow{b} \vert = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \sin{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Die Vektoren \(\overrightarrow{a}\), \(\overrightarrow{b}\) und \(\overrightarrow{c}\) bilden in dieser Reihenfolge ein Rechtssystem. Rechtehandregel: Weist \(\overrightarrow{a}\) in Richtung des Daumens und \(\overrightarrow{b}\) in Richtung des Zeigefingers, dann weist \(\overrightarrow{c} = \overrightarrow{a} \times \overrightarrow{b}\) in Richtung des Mittelfingers.
Berechnung eines Vektorprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \times \overrightarrow{b} = \begin {pmatrix} a_1 \\ a_2 \\ a_3 \end {pmatrix} \times \begin {pmatrix} b_1 \\ b_2 \\ b_3 \end {pmatrix} = \begin {pmatrix} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end {pmatrix}\]
Skalarprodukt
Unter dem Skalarprodukt \(\overrightarrow{a} \circ \overrightarrow{b}\) zweier Vektoren \(\overrightarrow{a}\) und \(\overrightarrow{b}\) versteht man das Produkt aus den Beträgen der beiden Vektoren und dem Kosinus des von den Vektoren eingeschlossenen Winkels \(\varphi\).
\[\overrightarrow{a} \circ \overrightarrow{b} = \vert \overrightarrow{a} \vert \cdot \vert \overrightarrow{b} \vert \cdot \cos{\varphi} \quad (0^{\circ} \leq \varphi \leq 180^{\circ})\]
Berechnung eines Skalarprodukts im \(\boldsymbol{\mathbb R^{3}}\) (vgl. Merkhilfe)
\[\overrightarrow{a} \circ \overrightarrow{b} = \begin{pmatrix} a_{1} \\ a_{2} \\ a_{3} \end{pmatrix} \circ \begin{pmatrix} b_{1} \\ b_{2} \\ b_{3} \end{pmatrix} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\]
\[ \begin {align*} V_{\text{Pyramide}} &= \frac{1}{6} \cdot \left| \left( \overrightarrow{FE} \times \overrightarrow{FG} \right) \circ \overrightarrow{FB}\, \right| \\[0.8em] &= \frac{1}{6} \cdot \left| \; \left[ \begin {pmatrix} -6 \\ 0 \\ 0 \end {pmatrix} \times \begin {pmatrix} 0 \\ 6 \\ 0 \end {pmatrix} \right] \circ \begin {pmatrix} 0 \\ 0 \\ -6 \end {pmatrix} \; \right| \\[0.8em] &= \frac{1}{6} \cdot \left| \; \begin {pmatrix} 0 & \cdot & 0 & - & 0 & \cdot & (-6) \\ 0 & \cdot & 0 & - & (-6) & \cdot & 0 \\ (-6) & \cdot & 6 & - & 0 & \cdot & 0 \end {pmatrix} \circ \begin {pmatrix} 0 \\ 0 \\ -6 \end {pmatrix} \; \right| \\[0.8em] &= \frac{1}{6} \cdot \left| \; \begin {pmatrix} 0 \\ 0 \\ -36 \end {pmatrix} \circ \begin {pmatrix} 0 \\ 0 \\ -6 \end {pmatrix} \; \right| \\[0.8em] &= \frac{1}{6} \cdot \vert 0 \cdot 0 + 0 \cdot 0 + (-36) \cdot (-6) \vert \\[0.8em] &= 36 \end {align*} \]
Anteil des Pyramidenvolumens am Würfelvolumen
Volumen des Würfels:
\[V_{Würfel} = 6 \cdot 6 \cdot 6 = 216\]
\[\frac{V_{\text{Pyramide}}}{V_{Würfel}} = \frac{36}{216} = \frac{1}{6} \approx 17\%\]
Die Pyramide nimmt ca. 17 % des Würfelvolumens ein.


