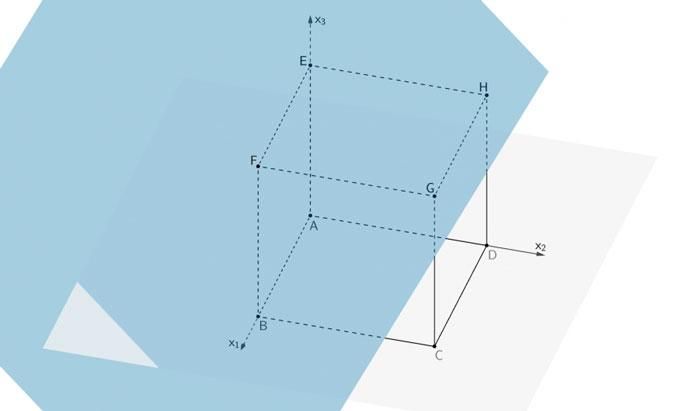
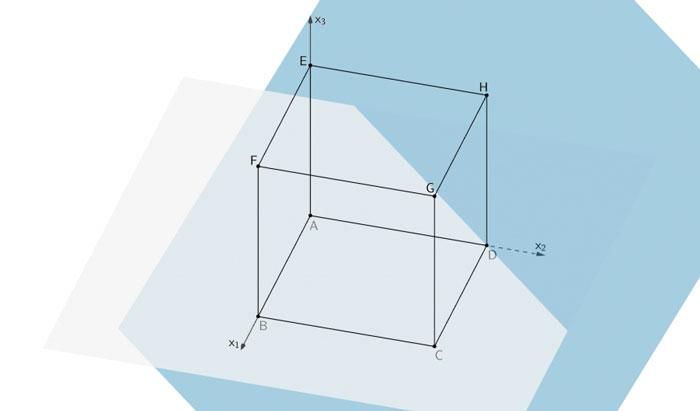
Jede Ebene, die parallel zu \(M\) verläuft, wird durch eine Gleichung der Form \(x_1 - x_2 + x_3 = p\) mit \(p \in \mathbb R\) beschrieben. Nennen Sie die Arten der Figuren, in denen eine solche Ebene den Würfel schneiden kann, und geben Sie die Menge aller Werte von \(p\) an, für die die Schnittfigur ein Sechseck ist.
(4 BE)
Lösung zu Teilaufgabe e
Ebenenschar \(x_{1} - x_{2} + x_{3} = p,\; p \in \mathbb R\)
Würfel \(ABCDEFGH\)
Arten von Schnittfiguren
Die Schnittfiguren, in denen eine Scharebene der Ebenenschar \(x_{1} - x_{2} + x_{3} = p,\; p \in \mathbb R\) den Würfel \(ABCDEFGH\) schneiden kann, sind: gleichseitiges Dreieck und Sechseck bzw. reguläres Sechseck.
Veranschaulichung (nicht verlangt)
Als Orientierung dienen die Ergebnisse und Informationen aus den Teilaufgaben a, c und d:
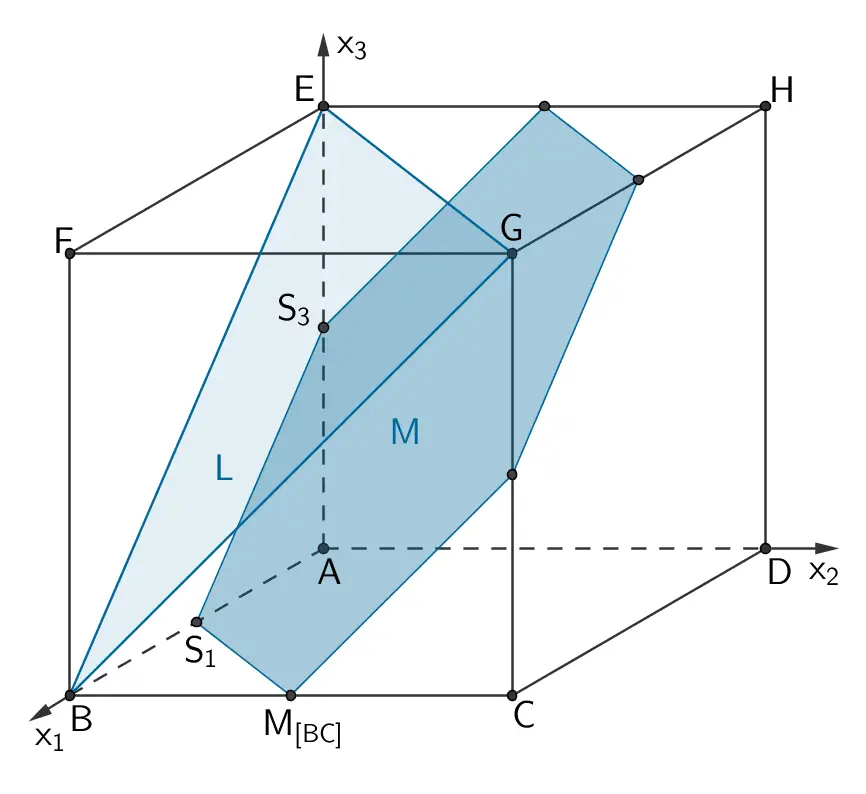
Die Schnittfigur, in der die Scharebene \(L\colon x_{1} - x_{2} + x_{3} = 6 \; (p = 6)\) den Würfel \(ABCDEFGH\) schneidet, ist ein gleichseitiges Dreieck (vgl. Teilaufgabe a).
Die Schnittfigur, in der die Scharebene \(M\colon x_{1} - x_{2} + x_{3} = 3 \; (p = 3)\) den Würfel \(ABCDEFGH\) schneidet, ist ein reguläres Sechseck (vgl. Teilaufgaben c und d).
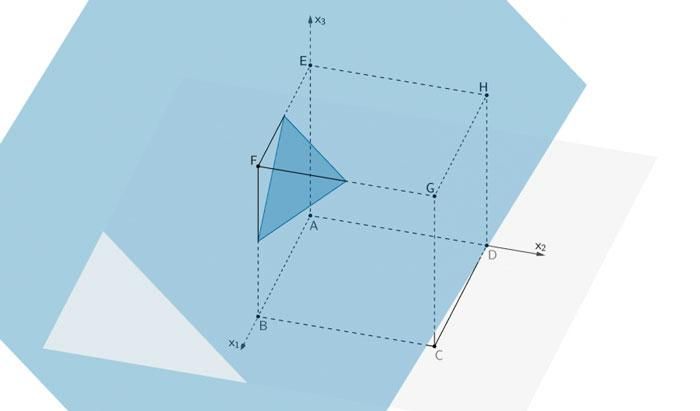
Wandert die Ebene \(L\) in Richtung des Punktes \(F\), ist die Schnittfigur ein gleichseitiges Dreieck
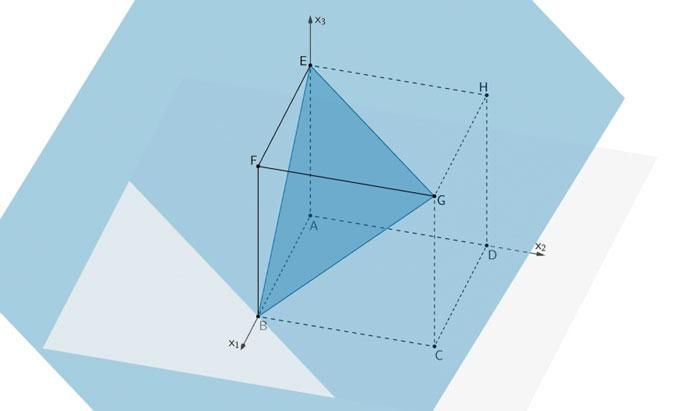
Die Schnittfigur, in der die Scharebene \(L\) den Würfel schneidet, ist ein gleichseitiges Dreieck.
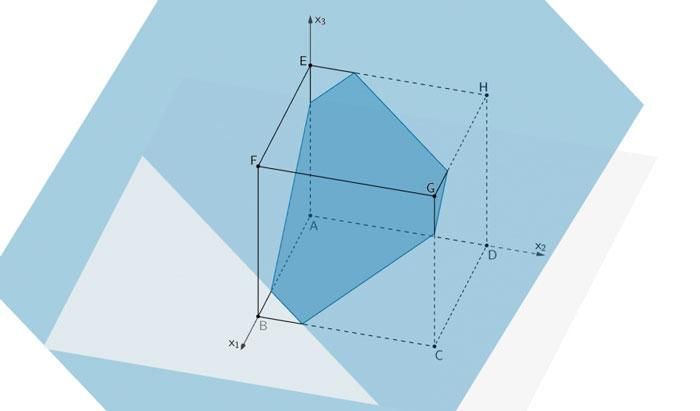
Wandert die Ebene \(L\) in Richtung der Ebene \(M\), ist die Schnittfigur ein Sechseck.
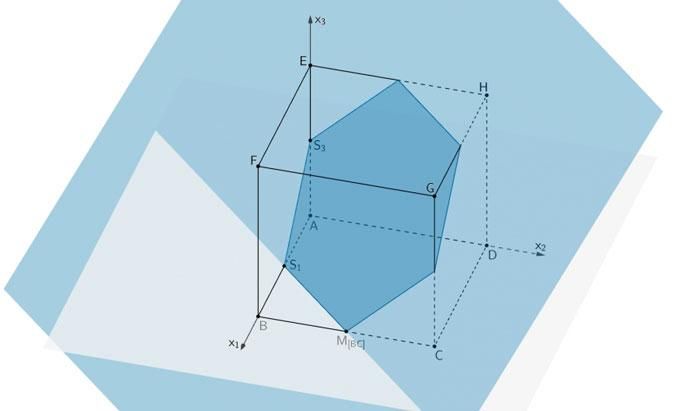
Die Schnittfigur, in der die Ebene M den Würfel Schneidet, ist ein reguläres Sechseck.
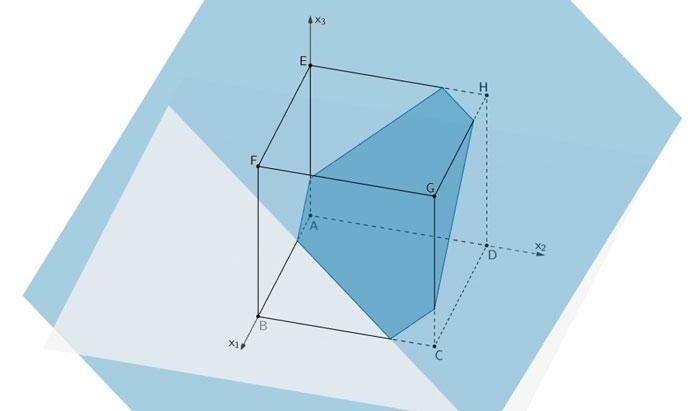
Wandert die Ebene \(M\) in Richtung des Punktes \(H\), ist die Schnittfigur ein Sechseck.
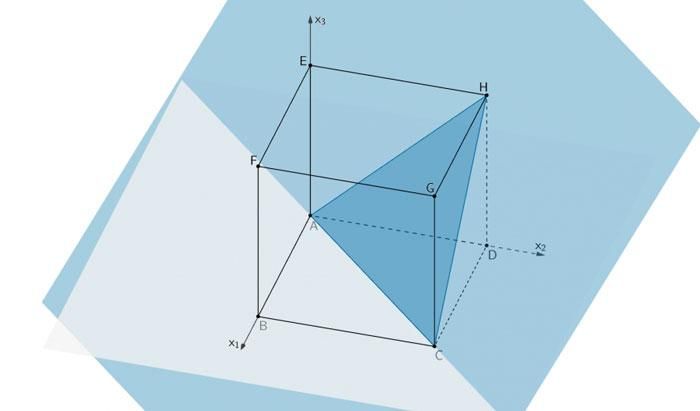
Enthält die Scharebene den Punkt \(H\), ist die Schnittfigur ein gleichseitiges Dreieck.
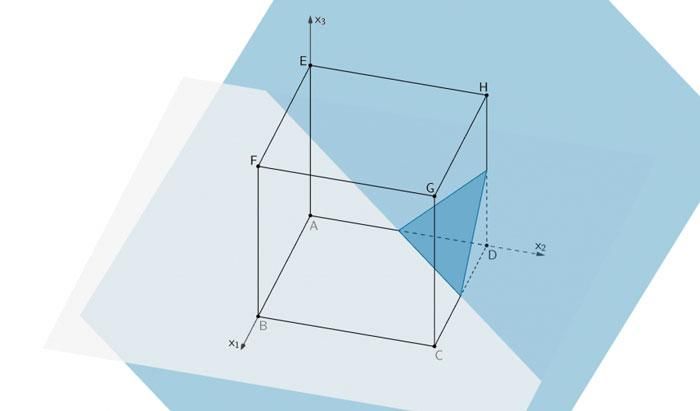
Wandert die Ebenenschar weiter in Richtung des Punktes D, ist die Schnittfigur ein gleichseitiges Dreieck.
Menge aller Werte von \(p\), für die die Schnittfigur ein Sechseck ist
Für \(p \in \; ]0; 6[\) sind die Schnittfiguren Sechsecke.
Begründung (nicht verlangt)
Ebenenschar \(x_{1} - x_{2} + x_{3} = p,\; p \in \mathbb R\)
Die Schnittfigur, in der die Scharebene \(L\colon x_{1} - x_{2} + x_{3} = 6 \; (p = 6)\) den Würfel \(ABCDEFGH\) schneidet, ist ein gleichseitiges Dreieck (vgl. Teilaufgabe a).
Die Schnittfigur, in der die Scharebene \(M\colon x_{1} - x_{2} + x_{3} = 3 \; (p = 3)\) den Würfel \(ABCDEFGH\) schneidet, ist ein reguläres Sechseck (vgl. Teilaufgaben c und d).
Für \(p \in [3;6[\) sind die Schnittfiguren somit Sechsecke.
Die Schnittfigur der Scharebene, welche den Punkt \(H\) enthält ist wieder ein gleichseitiges Dreieck.
Die Koordinaten von \(H(0|6|6)\) in die Gleichung der Ebenenschar eingesetzt, ergibt:
\[\begin{align*}0 - 6 + 6 &= p \\[0.8em] 0 &= p\end{align*}\]
Folglich sind die Schnittfiguren für \(p \in \; ]0; 6[\) Sechsecke.