Grenzwertbetrachtung

Begründen Sie mithilfe des Funktionsterms von \(f\), dass \(\lim \limits_{x \, \to \, -\infty} f(x) = 0\) und \(\lim \limits_{x \, \to \, +\infty} f(x) = 2\) gilt.

(2 BE)

Die Funktion \(g\) hat eine Funktionsgleichung der Form I, II oder III mit \(a \in \mathbb R \backslash \{0\}\):

Begründen Sie, dass weder eine Gleichung der Form I noch eine der Form II als Funktionsgleichung von \(g\) infrage kommt.

Die Funktionsgleichung von \(g\) hat also die Form III. Bestimmen Sie den passenden Wert von \(a\).

(5 BE)

Geben Sie das Verhalten von \(g\) für \(x \to -\infty\) und \(x \to +\infty\) an.

(2 BE)

Geben Sie den Term einer gebrochen-rationalen Funktion \(f\) mit Definitionsmenge \(\mathbb R \backslash \{-1\}\) an, deren Graph die Gerade mit der Gleichung \(y = 2\) als Asymptote besitzt und in \(x = -1\) eine Polstelle ohne Vorzeichenwechsel hat.

(3 BE)

Abbildung 2 zeigt den Graphen \(G_g\) einer in \(\mathbb R \backslash \{1\}\) definierten gebrochen-rationalen Funktion \(g\) mit folgenden Eigenschaften:

• Die Funktion \(g\) hat in \(x = 1\) eine Polstelle ohne Vorzeichenwechsel;

• \(G_g\) verläuft stets oberhalb seiner schrägen Asymptote, die durch die Gleichung \(y = \frac{1}{2}x - 1\) gegeben ist;

• die einzige Nullstelle von \(g\) ist \(x = -1\).

Abb. 2

Ermitteln Sie mithilfe von Abbildung 2 näherungsweise den Wert der Ableitung \(g'\) von \(g\) an der Stelle \(x = -1\); veranschaulichen Sie Ihr Vorgehen durch geeignete Eintragungen in der Abbildung.

Aus der Gleichung der schrägen Asymptote ergibt sich unmittelbar das Verhalten der Ableitung \(g'\) für \(x \to +\infty\) und \(x \to -\infty\). Geben Sie dieses Verhalten an und skizzieren Sie den Graphen von \(g'\) in Abbildung 2.

(6 BE)

Gegeben ist die Schar der Funktionen \(f_a : x \mapsto 6 \cdot e^{-0{,}5x} - a \cdot x\) mit \(a \in \mathbb R^+\) und Definitionsmenge \(\mathbb R\).

Weisen Sie nach, dass die Graphen aller Funktionen der Schar die \(y\)-Achse im selben Punkt schneiden und in \(\mathbb R\) streng monoton fallend sind. Zeigen Sie, dass \(\lim \limits_{x \, \to \, +\infty} f_a(x) = -\infty\) gilt.

(5 BE)

Gegeben ist die in \(\mathbb R\) definierte Funktion \(f \colon x \mapsto 2x \cdot e^{-0{,}5x^2}\). Abbildung 2 zeigt den Graphen \(G_f\) von \(f\).

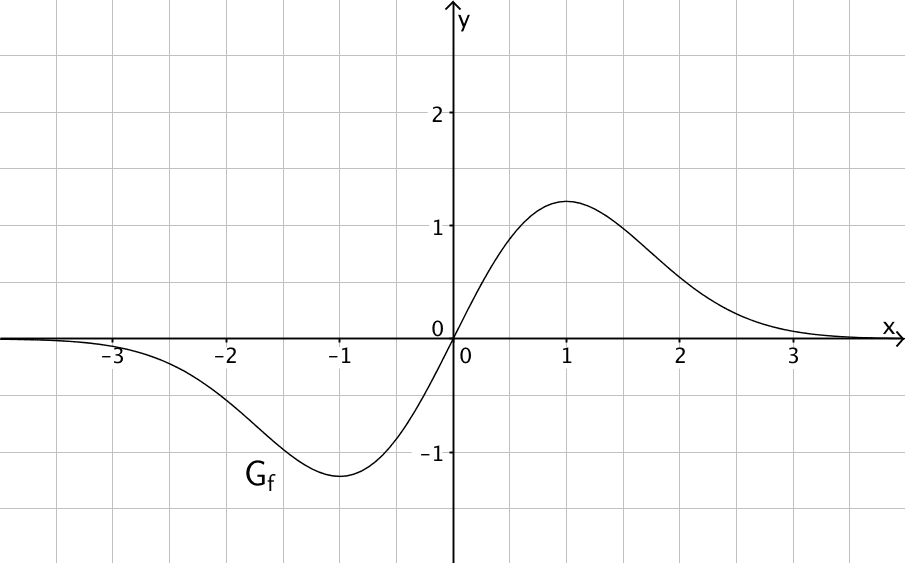Abb. 2

Weisen Sie nach, dass \(G_f\) punktsymmetrisch bezüglich des Koordinatenursprungs ist, und machen Sie anhand des Funktionsterms von \(f\) plausibel, dass \(\lim \limits_{x \, \to \, + \infty} f(x) = 0\) gilt.

(2 BE)

Der Graph von \(f\), die \(x\)-Achse und die Gerade \(x = u\) mit \(u \in \mathbb R^+\) schließen für \(0 \leq x \leq u\) ein Flächenstück mit dem Inhalt \(A(u)\) ein.

Zeigen Sie, dass \(A(u) = 2 - 2e^{-0{,}5u^2}\) gilt. Geben Sie \(\lim \limits_{u \, \to \, + \infty} A(u)\) an und deuten Sie das Ergebnis geometrisch.

(6 BE)

Im Folgenden wird die Schar der in \(\mathbb R\) definierten Funktionen \(g_c \colon x \mapsto f(x) + c\) mit \(c \in \mathbb R\) betrachtet.

Geben Sie in Abhängigkeit von \(c\) ohne weitere Rechnung die Koordinaten des Hochpunkts des Graphen von \(g_c\) sowie das Verhalten von \(g_c\) für \(x \to + \infty\) an.

(2 BE)

Welche künftige Entwicklung der Bevölkerungszahl ist auf der Grundlage des Modells zu erwarten? Begründen Sie Ihre Antwort.

(2 BE)

Im betrachteten Zeitraum gibt es ein jahr, in dem die Geburtenziffer am stärksten abnimmt. Geben Sie mithilfe von Abbildung 2 einen Näherungswert für dieses Jahr an. Beschreiben Sie, wie man auf der Grundlage des Modells rechnerisch nachweisen könnte, dass die Abnahme der Geburtenziffer von diesem Jahr an kontinuierlich schwächer wird.

(3 BE)

Geben Sie für die Funktion \(f\) mit \(f(x) = \ln (2013 - x)\) den maximalen Definitionsbereich \(D\), das Verhalten von \(f\) an den Grenzen von \(D\) sowie die Schnittpunkte des Graphen von \(f\) mit den Koordinatenachsen an.

(5 BE)

Gegeben sind die in \(\mathbb R\) definierten Funktionen \(g \colon x \mapsto e^{-x}\) und \(h \colon x \mapsto x^3\).

Veranschaulichen Sie durch eine Skizze, dass die Graphen von \(g\) und \(h\) genau einen Schnittpunkt haben.

(2 BE)

Gegeben ist die Funktion \(\displaystyle f \colon x \mapsto \frac{1}{2}x - \frac{1}{2} + \frac{8}{x + 1}\) mit Definitionsbereich \(\mathbb R \backslash \{-1\} \).

Abbildung 2 zeigt den Graphen \(G_f\) von \(f\).

Abb. 2

Geben Sie die Gleichungen der Asymptoten von \(G_f\) an und zeigen Sie rechnerisch, dass \(G_f\) seine schräge Asymptote nicht schneidet. Zeichnen Sie die Asymptoten in Abbildung 2 ein.

(6 BE)

Ermitteln Sie das Symmetrieverhalten des Graphen von \(f\) und geben Sie den Grenzwert von \(f\) für \(x \to +\infty\) an.

(3 BE)

Geben Sie das Verhalten von \(f\) für \(x \to -\infty\) an. Machen Sie plausibel, dass \(G_f\) für \(x \to +\infty\) die Gerade mit der Gleichung \(y = x\) als schräge Asymptote besitzt.

(3 BE)

Für \(x \geq 0\) beschreibt die Funktion \(h\) modelhaft die zeitliche Entwicklung des momentanen Schadstoffausstoßes einer Maschine. Dabei ist \(x\) die seit dem Start der Maschine vergangene Zeit in Minuten und \(h(x)\) die momentane Schadstoffausstoßrate in Milligramm pro Minute.

Geben Sie in diesem Sachzusammenhang die Bedeutung des Monotonieverhaltens von \(G_h\) sowie des Grenzwerts von \(h\) für \(x \to +\infty\) an.

(3 BE)