Auf der Autobahn entsteht morgens an einer Baustelle häufig ein Stau.
An einem bestimmten Tag entsteht der Stau um 06:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Tag kann die momentane Änderungsrate der Staulänge mithilfe der in \(\mathbb R\) definierten Funktion \(f\) mit
\(f(x) = x \cdot (8 - 5x) \cdot \left( 1 - \frac{x}{4} \right)^2 = -\frac{5}{16}x^4 + 3x^3 - 9x^2 + 8x\)
beschrieben werden. Dabei gibt \(x\) die nach 06:00 Uhr vergangene Zeit in Stunden und \(f(x)\) die momentane Änderungsrate der Staulänge in Kilometern pro Stunde an. Die Abbildung 1 zeigt den Graphen von \(f\) für \(0 \leq x \leq 4\).
Für die erste Ableitungsfunktion von \(f\) gilt \(f'(x) = (5x^2-16x+8) \cdot \left( 1 - \frac{x}{4} \right)\).
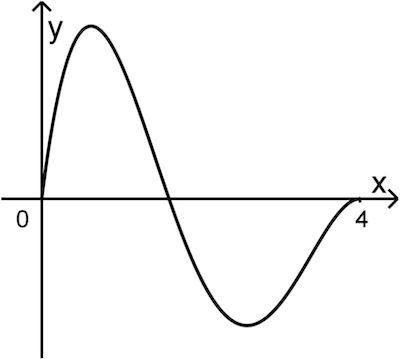Abb. 1
Nennen Sie die Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat, und begründen Sie anhand der Struktur des Funktionsterms von \(f\), dass es keine weitere solchen Zeitpunkte gibt.
(3 BE)
Lösung zu Teilaufgabe 1a
\[f(x) = x \cdot (8 - 5x) \cdot \left( 1 - \frac{x}{4} \right)^2 = -\frac{5}{16}x^4 + 3x^3 - 9x^2 + 8x\]
Zeitpunkte, zu denen die momentane Änderungsrate der Staulänge den Wert null hat
06:00 Uhr, 07:36 Uhr und 10:00 Uhr
Begründung (nicht verlangt)
Die Funktion \(f\) beschreibt die momentane Änderungsrate der Staulänge. Diese soll den Wert null haben, also sind die Nullstellen von \(f\) zu betrachten.
Nullstelle(n) einer Funktion bestimmen
Eine Nullstelle ist die \(x\)-Koordinate eines gemeinsamen Punktes des Graphen einer Funktion \(x \mapsto f(x)\) mit der \(x\)-Achse. An einer Nullstelle gilt: \(f(x) = 0\).
Satz vom Nullprodukt: Ein Produkt ist genau dann null, wenn einer der Faktoren null ist.
\(f(x) \cdot g(x) = 0 \enspace \Rightarrow \enspace f(x) = 0\) oder \(g(x) = 0\)
Ein Quotient von Funktionen ist genau dann null, wenn die Zählerfunktion null ist.
\(\dfrac{f(x)}{g(x)} = 0 \enspace \Rightarrow \enspace f(x) = 0\; (g(x) \neq 0)\)
Lösungsformel für quadratische Gleichungen (Mitternachtsformel, vgl. Merkhilfe)
\[\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x + \textcolor{#e9b509}{c} = 0 \enspace \Leftrightarrow \enspace x_{1,2} = \frac{-\textcolor{#0087c1}{b} \pm \sqrt{\textcolor{#0087c1}{b}^2 - 4\textcolor{#cc071e}{a}\textcolor{#e9b509}{c}}}{2\textcolor{#cc071e}{a}}\]
Diskriminante \(D = b^2 -4ac \;\):
\(D < 0\,\): keine Lösung
\(D = 0\,\): genau eine Lösung
\(D > 0\,\): zwei verschiedene Lösungen
Folgende Fälle lassen sich einfacher durch Umformung lösen:
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#0087c1}{b}x &= 0 &&| \; x\; \text{ausklammern (Produkt formulieren)} \\[0.8em] x \cdot (ax + b) &= 0 \\[0.8em] \Rightarrow \enspace x = 0 \vee ax + b &= 0 \end{align*}\]
\[\begin{align*}\textcolor{#cc071e}{a}x^2 + \textcolor{#e9b509}{c} &= 0 &&| -c \enspace (c \neq 0) \\[0.8em] ax^2 &= -c &&| : a \\[0.8em] x^2 &= -\frac{c}{a} &&| \; \sqrt{\quad} \\[0.8em] x_{1,2} &= \pm \sqrt{-\frac{c}{a}} \end{align*}\]
Zwei Lösungen, falls \(-\dfrac{c}{a} > 0\), keine Lösung, falls \(-\dfrac{c}{a} < 0\)
Vorgehensweise für die Bestimmung der Nullstelle(n) einer ganzrationalen Funktion ab Grad 3:
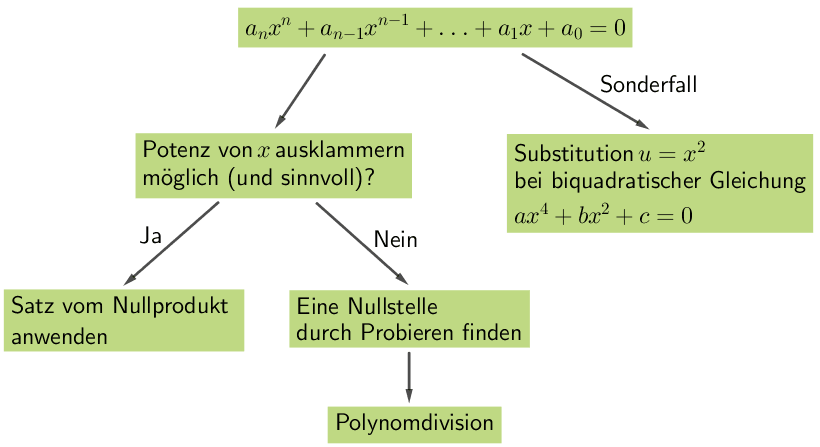
vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen
Nullstellen einer gebrochenrationalen Funktion \(f(x) = \dfrac{\textcolor{#0087c1}{z(x)}}{n(x)}\) sind alle Nullstellen des Zählerpolynoms \(\textcolor{#0087c1}{z(x)}\), die nicht zugleich Nullstellen des Nennerpolynoms \(\boldsymbol{n(x)}\) sind.
Ist \(x_0\) eine Nullstelle des Zählerpolynoms \(\boldsymbol{z(x)}\) und zugleich eine vollständig kürzbare Nullstelle des Nennerpolynoms \(\boldsymbol{n(x)}\), so besitzt die gebrochenrationale Funktion \(f\) an der Stelle \(x_0\) eine hebbare Definitionslücke.
(vgl. Abiturskript - 1.2.1 Gebrochenrationale Funktion, Nullstellen und Polstellen)
Eine Wurzelfunktion \(f(x) = \sqrt{\textcolor{#cc071e}{g(x)}}\) nimmt genau dann den Wert null an, wenn der Radikand (Term unter der Wurzel) null ist.
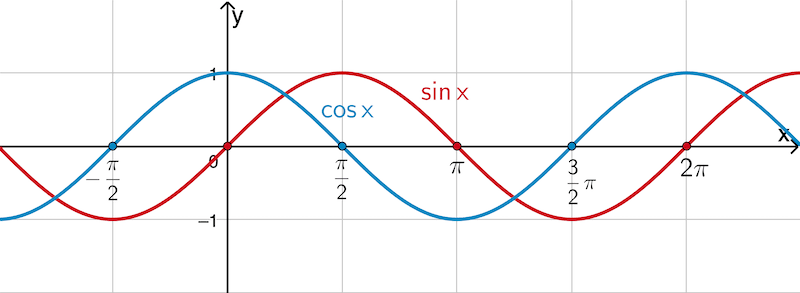
\[\sin{x} = 0 \enspace \Rightarrow \enspace x = k \cdot \pi \; (k \in \mathbb Z)\]
\[\cos{x} = 0 \enspace \Rightarrow \enspace x = \dfrac{\pi}{2} + k \cdot \pi \; (k \in \mathbb Z)\]
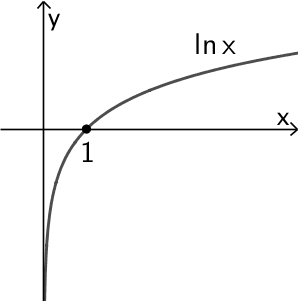
Die natürliche Logarithmusfunktion \(x \mapsto \ln{x}\) besitzt die einzige Nullstelle \(\boldsymbol{x = 1}\).
\[\ln{\left( \textcolor{#0087c1}{f(x)} \right)} = 0 \enspace \Rightarrow \enspace \textcolor{#0087c1}{f(x) = 1}\]
Die natürliche Exponentialfunktion \(x \mapsto e^x\) sowie jede verkettete Funktion \(x \mapsto e^{f(x)}\) besitzt keine Nullstelle!
\[\begin{align*}f(x) &= 0 \\[0.8em] \textcolor{#e9b509}{x} \cdot \textcolor{#cc071e}{(8 - 5x)} \cdot \textcolor{#0087c1}{\left( 1 - \frac{x}{4} \right)}^2 &= 0\end{align*}\]
\[\Rightarrow \textcolor{#e9b509}{x_1 = 0}\; \vee \; \textcolor{#cc071e}{x_2 = \frac{8}{5} = 1{,}6}\; \vee \; \textcolor{#0087c1}{x_3 = 4}\]
\(x\) gibt die nach 06:00 Uhr vergangene Zeit in Stunden an (vgl. Angabe).
\(x_1 = 0\) bedeutet 0 Stunden nach 06:00 Uhr, also 06:00 Uhr.
\(x_2 = 1{,}6\) bedeutet \(1{,}6 \cdot 60\;\text{min} = 96\;\text{min} = 1\;\text{h}\;36\;\text{min}\) nach 06:00 Uhr, also 07:36 Uhr.
\(x_3 = 4\) bedeutet 4 Stunden nach 06:00 Uhr, also 10:00 Uhr.
Begründung anhand des Funktionsterms, dass es keine weiteren solchen Zeitpunkte gibt
\(f\) ist eine ganzrationale Funktion 4. Grades, die maximal vier Nullstellen besitzen kann. \(f\) hat zwei einfachen Nullstellen \(\textcolor{#e9b509}{x_1 = 0}\) und \(\textcolor{#cc071e}{x_2 = 1{,}6}\) sowie die doppelte Nullstelle \(\textcolor{#0087c1}{x_3 = 4}\), also insgesamt vier Nullstellen. Folglich kann es keine weitere Nullstelle geben und damit keinen weiteren Zeitpunkt, zu dem die momentane Änderungsrate der Staulänge den Wert null hat.
(vgl. Abiturskript - 1.1.3 Ganzrationale Funktion, Nullstellen)
