Tatsächlich ist der Anteil der Beschäftigten mit einem Jobticket an beiden Standorten unterschiedlich; am Standort B besitzt nur die Hälfte der Beschäftigten ein Jobticket. Berechnen Sie die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers, der ein Jobticket besitzt, am Standort A arbeitet.
(3 BE)
Lösung zu Teilaufgabe 3b
\[P(A \cap J) = P(J) - P(B \cap J) = 0{,}6 - 0{,}2 \cdot 0{,}5 = 0{,}5\]
\[P_J(A) = \frac{P(A \cap J)}{P(J)} = \frac{0{,}5}{0{,}6} = \frac{5}{6}\]
Ausführliche Erklärung (nicht verlangt)
\(A\): „Beschäftigte(r) am Strandort A"
\(B\): „Beschäftigte(r) am Strandort B"
\(J\): „Beschäftigte(r) besitzt ein Jobticket."
\(\overline{J}\): „Beschäftigte(r) besitzt kein Jobticket."
Analyse der Angabe
„...am Standort B besitzt nur die Hälfte der Beschäftigten ein Jobticket."
\(\Rightarrow\;P_B(J) = 0{,}5\)
Außerdem bereits bekannt (vgl. Angabe Aufgabe 3, Teilaufgabe 1a)
\(P(B) = 0{,}2\); \(P(J) = 0{,}6\)
„Berechnen Sie die Wahrscheinlichkeit dafür, dass ein ... Beschäftigter ..., der ein Jobticket besitzt, am Standort A arbeitet."
Gesucht ist die bedingte Wahrscheinlichkeit \(P_J(A)\)
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[P_J(A) = \frac{P(A \cap J)}{P(J)}\]
Zunächst ist die Wahrscheinlichkeit \(P(A \cap J)\) zu berechnen.
Veranschaulichung mithilfe eines Baumdiagramms
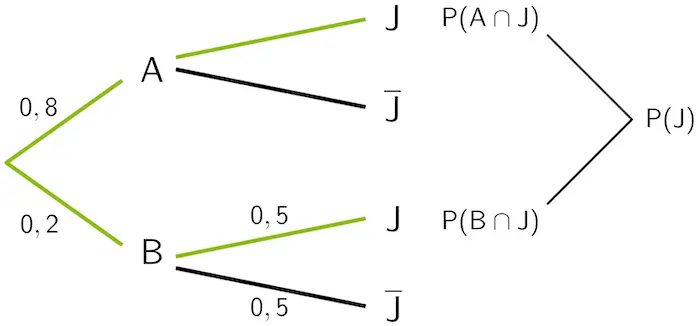
Pfadregeln
Verzweigungsregel (Knotenregel)
Die Summe der Wahrscheinlichkeiten an den Ästen, die von einem Knoten ausgehen, ist gleich eins.
1. Pfadregel (Produktregel)
Die Wahrscheinlichkeit eines Ergebnisses ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu dem Ergebnis führt.
2. Pfadregel (Summenregel)
Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Wahrscheinlichkeiten der Ergebnisse, die zu diesem Ereignis gehören.
2. Padregel (Summenregel) anwenden:
\[\begin{align*}P(A \cap J) + P(B \cap J) &= P(J) &&| - P(B \cap J) \\[0.8em] P(A \cap J) &= P(J) - P(B \cap J) \\[0.8em] &= 0{,}6 - 0{,}2 \cdot 0{,}5 \\[0.8em] &= 0{,}6 - 0{,}1 \\[0.8em] &= 0{,}5 \end{align*}\]
Damit ergibt sich:
\[P_J(A) = \frac{P(A \cap J)}{P(J)} = \frac{0{,}5}{0{,}6} = \frac{5}{6} \approx 0{,}833 = 83{,}3\,\%\]
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers, der ein Jobticket besitzt, am Standort A arbeitet, beträgt \(\dfrac{5}{6}\).
Alternative: Vierfeldertafel (bekannt)
| \(A\) | \(B\) | ||
| \(J\) | \(\textcolor{#89ba17}{0{,}6}\) | ||
| \(\overline{J}\) | \(\textcolor{#89ba17}{0{,}4}\) | ||
| \(\textcolor{#89ba17}{0{,}8}\) | \(\textcolor{#89ba17}{0{,}2}\) | \(1\) |
Sofern aus Teilaufgabe 1a noch kein innerer Eintrag der Vierfeldertafel bekannt ist, lässt sich dieser mithilfe der gegebenen bedingten Wahrscheinlichkeit \(P_B(J) = 0{,}5\) ermitteln.
Bedingte Wahrscheinlichkeit
Die Wahrscheinlichkeit für das Eintreten des Ereignisses \(B\) unter der Voraussetzung oder der Bedingung, dass das Ereignis \(A\) bereits eingetreten ist, heißt bedingte Wahrscheinlichkeit von \(\boldsymbol{B}\) unter der Bedingung \(\boldsymbol{A}\) und wird durch die Schreibweise \(P_{A}(B)\) gekennzeichnet.
Es gilt: \(P_{A}(B) = \dfrac{P(A \cap B)}{P(A)} \quad (P(A) \neq 0)\)
(vgl. Merkhilfe)
\[\begin{align*} P_B(J) &= \frac{P(B \cap J)}{P(B)} &&| \cdot P(B) \\[0.8em] P(B \cap J) &= P(B) \cdot P_B(J) \\[0.8em] &= 0{,}2 \cdot 0{,}5 = 0{,}1 \end{align*}\]
| \(A\) | \(B\) | ||
| \(J\) | \(0{,}1\) | \(\textcolor{#89ba17}{0{,}6}\) | |
| \(\overline{J}\) | \(\textcolor{#89ba17}{0{,}4}\) | ||
| \(\textcolor{#89ba17}{0{,}8}\) | \(\textcolor{#89ba17}{0{,}2}\) | \(1\) |
Nun kann die Wahrscheinlichkeit \(P(A \cap J)\) und anschließend die gesuchte bedingte Wahrscheinlichkeit \(P_J(A)\) berechnet werden.
\[P(A \cap J) = P(J) - P(B \cap J) = 0{,}6 - 0{,}1 = 0{,}5\]
| \(A\) | \(B\) | ||
| \(J\) | \(0{,}5\) | \(0{,}1\) | \(\textcolor{#89ba17}{0{,}6}\) |
| \(\overline{J}\) | \(\textcolor{#89ba17}{0{,}4}\) | ||
| \(\textcolor{#89ba17}{0{,}8}\) | \(\textcolor{#89ba17}{0{,}2}\) | \(1\) |
\[P_J(A) = \frac{P(A \cap J)}{P(J)} = \frac{0{,}5}{0{,}6} = \frac{5}{6} \approx 0{,}833 = 83{,}3\,\%\]
Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Beschäftigter des Autozulieferers, der ein Jobticket besitzt, am Standort A arbeitet, beträgt \(\dfrac{5}{6}\).

