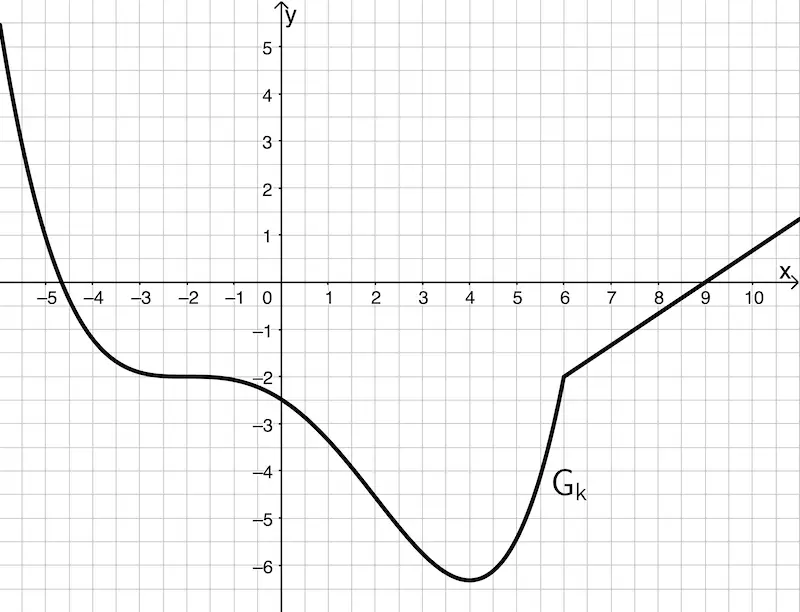
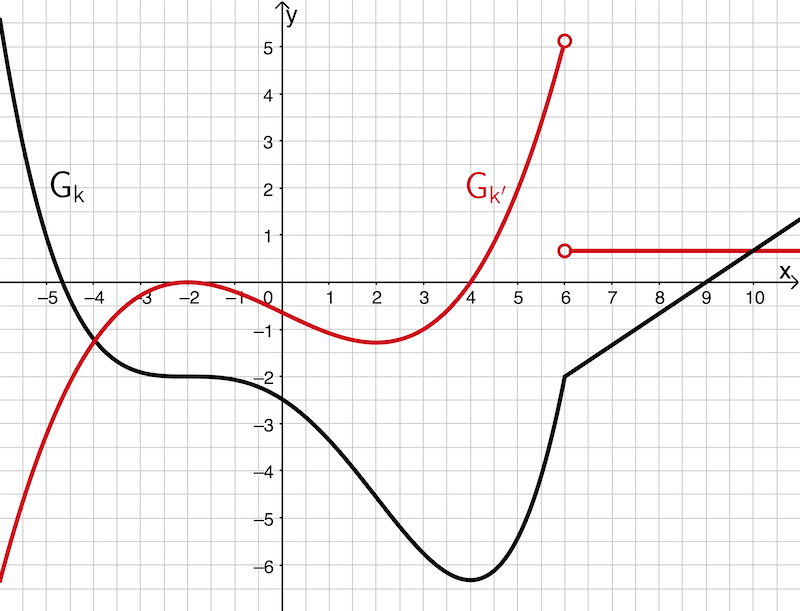
Die Abbildung zeigt den Graphen \(G_k\) einer Funktion \(k\).
a) Begründen Sie, dass \(k\) an der Stelle \(x = 6\) nicht differenzierbar ist, indem Sie mithilfe der Abbildung zugehörige Grenzwerte angeben und daraus schlussfolgern.
b) Skizzieren Sie in der Abbildung den Graphen der Ableitungsfunktion \(k'\). Achten Sie auf ausreichende Genauigkeit.
a) Begründung mithilfe der Abbildung, dass \(k\) an der Stelle \(x = 6\) nicht differenzierbar ist
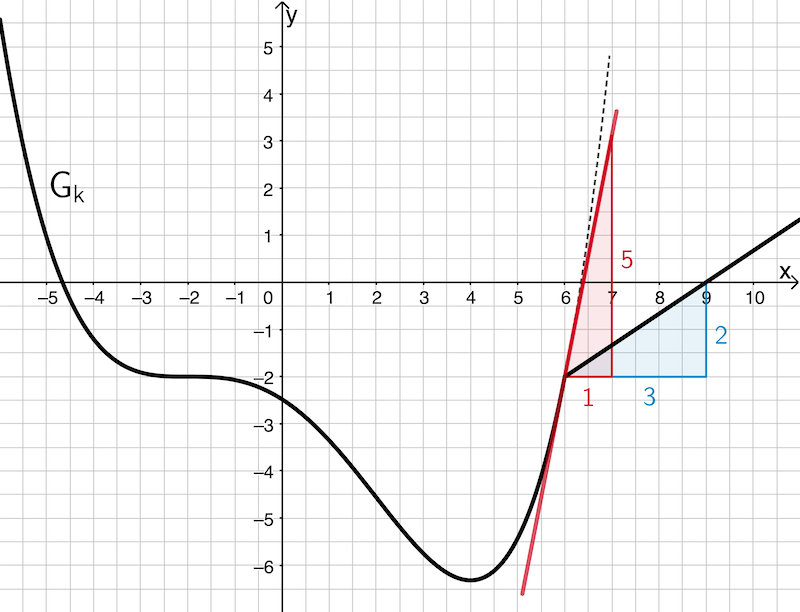
\[\underbrace{\lim \limits_{\textcolor{#cc071e}{\underset{x \,< \,6}{x\, \to\, 6}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#cc071e}{\text{linksseitiger Grenzwert}}}} \approx \textcolor{#cc071e}{5}\]
\[\underbrace{\lim \limits_{\textcolor{#0087c1}{\underset{x \,> \,6}{x\, \to\, 6}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#0087c1}{\text{rechtsseitiger Grenzwert}}}} = \textcolor{#0087c1}{\frac{2}{3}}\]
Da der linksseitige und der rechtsseitige Grenzwert des Differentialquotienten an der Stelle \(x = 6\) nicht übereinstimmen, ist die Funktion \(k\) an der Stelle \(x = 6\) nicht differenzierbar.
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Ausführliche Erklärung (nicht verlangt)
Eine Funktion ist an einer Stelle \(x_0\) differenzierbar („ableitbar"), wenn der Differentialquotient an der Stelle \(x_0\) existiert. Dafür müssen der linksseitige und der rechtsseitige Grenzwert des Differentialquotienten übereinstimmen.
Differentialquotient oder lokale bzw. momentane Änderungsrate
Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
Der Differentialquotient ist die formale Definition der Ableitung. In graphischer Interpretation bedeutet der Differentialquotient die Steigung des Graphen einer Funktion an einer betrachteten Stelle \(x_0\). Das heißt, die Steigung der Tangente an den Graphen an einer Stelle \(x_0\).
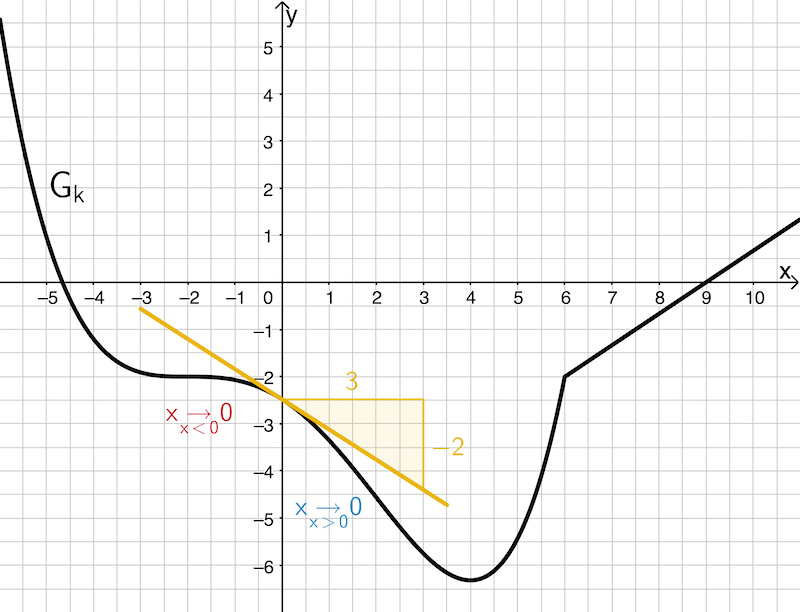
Beispielsweise lässt sich für den Graphen von \(k\) sowohl bei linksseitiger Annäherung als auch bei rechtsseitiger Annäherung an die Stelle \(x = 0\) eine eindeutige Tangentensteigung angeben, die graphisch ermittelt näherungsweise \(\textcolor{#e9b509}{-\dfrac{2}{3}}\) beträgt. Und es gilt:
\[\underbrace{\lim \limits_{\textcolor{#cc071e}{\underset{x\,<\,0}{x\,\to\,0}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#cc071e}{\text{linksseitiger Grenzwert}}}} = \underbrace{\lim \limits_{\textcolor{#0087c1}{\underset{x\,>\,0}{x\,\to\,0}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#0087c1}{\text{rechtsseitiger Grenzwert}}}} \approx \textcolor{#e9b509}{-\frac{2}{3}}\]
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Da der linksseitige und der rechtsseitige Grenzwert des Differentialquotienten an der Stelle \(x = 0\) übereinstimmen, ist die Funktion \(k\) an der Stelle \(x = 0\) differenzierbar.

An der „Knickstelle" \(x = 6\) existiert keine eindeutige Tangente. Hier ergibt sich bei linksseitiger Annäherung eine Steigung von etwa \(\textcolor{#cc071e}{5}\) und bei rechtsseitiger Annäherung eine Steigung von \(\textcolor{#0087c1}{\dfrac{2}{3}}\).
Die Aufgabenstellung erfordert, den „Knick" des Graphen von \(k\) an der Stelle \(x = 6\) mithilfe zugehöriger Grenzwerte zu beschreiben. Diese sind der linksseitige und der rechtsseitige Grenzwert des Differentialquotienten.
Differentialquotient oder lokale bzw. momentane Änderungsrate

Der Differentialquotient oder die lokale bzw. momentane Änderungsrate \(m_{x_{0}} = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\) beschreibt den Grenzwert des Differenzenquotienten \(\dfrac{f(x) - f(x_{0})}{x - x_{0}}\) bei beliebig genauer Annäherung \(x \to x_{0}\) und damit die Steigung der Tangente an den Graphen der Funktion \(f\) an der Stelle \(x_{0}\).
Man nennt den Grenzwert \(m_{x_{0}}\) die Ableitung von \(f\) an der Stelle \(x_{0}\) und schreibt dafür \(f'(x_{0})\). Voraussetzung: Der Grenzwert existiert an der Stelle \(x_{0}\) und ist endlich.
\[f'(x_{0}) = \lim \limits_{x \, \to \, x_{0}} \dfrac{f(x) - f(x_{0})}{x - x_{0}}\]
(vgl. Merkhilfe)
\[\underbrace{\lim \limits_{\textcolor{#cc071e}{\underset{x \,< \,6}{x\, \to\, 6}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#cc071e}{\text{linksseitiger Grenzwert}}}} \approx \textcolor{#cc071e}{5}\]
\[\underbrace{\lim \limits_{\textcolor{#0087c1}{\underset{x \,> \,6}{x\, \to\, 6}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#0087c1}{\text{rechtsseitiger Grenzwert}}}} = \textcolor{#0087c1}{\frac{2}{3}}\]
Differenzierbarkeit
Existiert für eine Funktion \(f\) an der Stelle \(x_0\) der Differentialquotient
\(\displaystyle f'(x_0) \, = \, \lim \limits_{x\,\to\,x_0} \frac{f(x) - f(x_0)}{x - x_0} \, = \, \lim \limits_{h\,\to\,0} \frac{f(x_0 + h) - f(x_0)}{h}\,\),
heißt die Funktion \(f\) differenzierbar an der Stelle \(\bf{x_0}\).
Der Differentialquotient existiert, wenn der linksseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#cc071e}{x\,<\,x_0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#cc071e}{h\,<\,0}}{h\,\to\,0}\)) und der rechtsseitige Grenzwert des Differentialquotienten (\(\underset{\textcolor{#0087c1}{x\,>\,0}}{x\,\to\,x_0}\) bzw. \(\underset{\textcolor{#0087c1}{h\,>\,0}}{h\,\to\,0}\)) übereinstimmen.
Daraus ergibt sich folgende Schlussfolgerung:
Da der linksseitige und der rechtsseitige Grenzwert des Differentialquotienten an der Stelle \(x = 6\) nicht übereinstimmen, ist die Funktion \(k\) an der Stelle \(x = 6\) nicht differenzierbar.
b) Skizzieren des Graphen der Ableitungsfunktion \(k'\)
Ausführliche Erklärung (nicht verlangt)
Die erste Ableitung einer Funktion beschreibt die Steigung einer Tangente an den Graphen der Funktion. Der Graph der Ableitungsfunktion \(k'\) stellt also den Verlauf der Tangentensteigung einer Tangente an den Graphen von \(k\) dar.
Für eine ausreichend genaue Skizze sind
- die Stellen, an denen der Graph von \(k\) eine waagrechte Tangente hat,
- die Stelle, an der die Steigung des Graphen von \(k\) ein lokales Minimum hat,
- die „Knickstelle" bei \(x = 6\) und
- der Verlauf des Graphen von \(k\) für \(x \to -\infty\) bzw. \(x \to +\infty\)
von besonderer Bedeutung.
Stellen, an denen der Graph von \(\boldsymbol{k}\) eine waagrechte Tangente hat
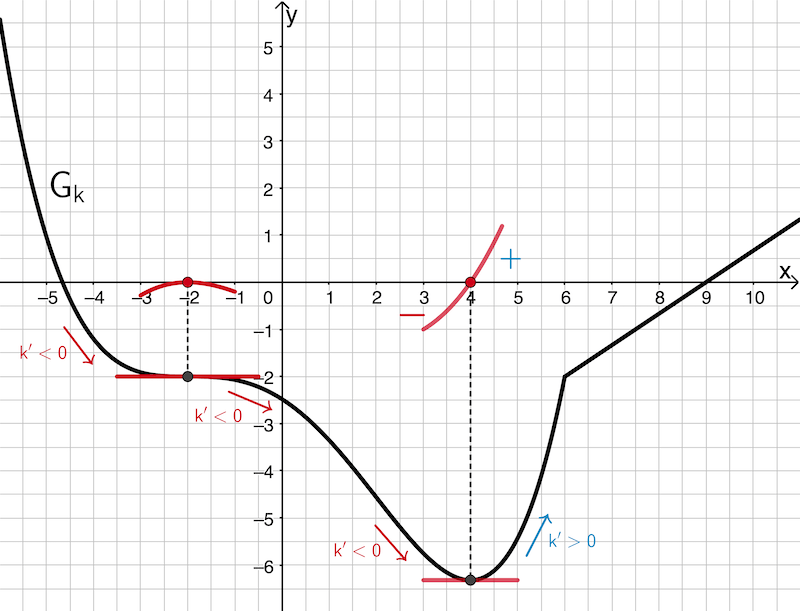
Der Graph von \(k\) hat im Terrassenpunkt an der Stelle \(x = -2\) eine waagrechte Tangente und damit die Steigung \(\textcolor{#cc071e}{m = 0}\). In der Umgebung des Terrassenpunkts ist \(G_k\) streng monoton fallend. Nach dem Monotoniekriterium gilt \(\textcolor{#cc071e}{k' < 0}\).
Anwendung der Differetialrechnung:
Monotoniekriterium
\(f'(x) < 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) fällt streng monoton in \(I\)
\(f'(x) > 0\) im Intervall \( I \enspace \Rightarrow \enspace G_{f}\) steigt streng monoton in \(I\)
(vgl. Merkhilfe)
Somit hat der Graph von \(\textcolor{#cc071e}{k'}\) bei \(x = -2\) eine Nullstelle ohne Vorzeichenwechsel und verläuft in deren Umgebung unterhalb der \(\textcolor{#cc071e}{x}\)-Achse.
Im Terrassenpunkt ist die Steigung von \(G_k\) mit \(\textcolor{#cc071e}{m = 0}\) maximal (weil \(G_k\) fällt). Der Graph von \(\textcolor{#cc071e}{k'}\) erreicht deshalb im Punkt \(\textcolor{#cc071e}{(-2|0)}\) ein lokales Maximum (relativer Hochpunkt).
Im Tiefpunkt an der Stelle \(x = 4\) hat der Graph von \(k\) ebenfalls eine waagrechte Tangente (\(\textcolor{#cc071e}{m = 0}\)) und wechselt dort das Monotonieverhalten von streng monoton fallend zu streng monoton steigend. Somit ist \(x = 4\) eine einfache Nullstelle des Graphen von \(k'\) mit Vorzeichenwechsel von \(\textcolor{#cc071e}{–}\) nach \(\textcolor{#0087c1}{+}\).
Stelle, an der die Steigung des Graphen von \(\boldsymbol{k}\) ein lokales Minimum hat
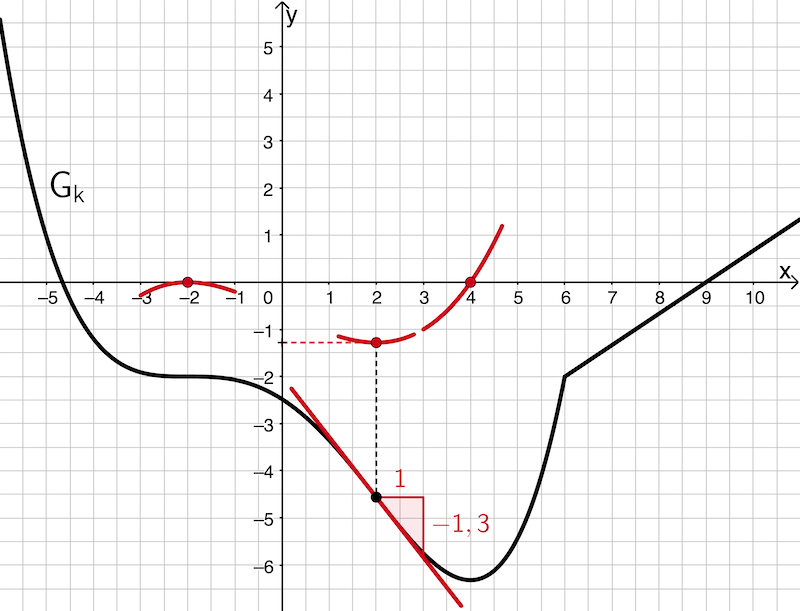
An der Wendestelle \(x = 2\) erreicht die Steigung des Graphen von \(k\) mit \(\textcolor{#cc071e}{m \approx -1{,}3}\) ein lokales Minimum (Steigung ist lokal maximal negativ). Der Graph von \(k'\) hat deshalb in etwa den relativen Tiefpunkt \((2|\textcolor{#cc071e}{-1{,}3})\).
„Knickstelle" bei \(\boldsymbol{x = 6}\)
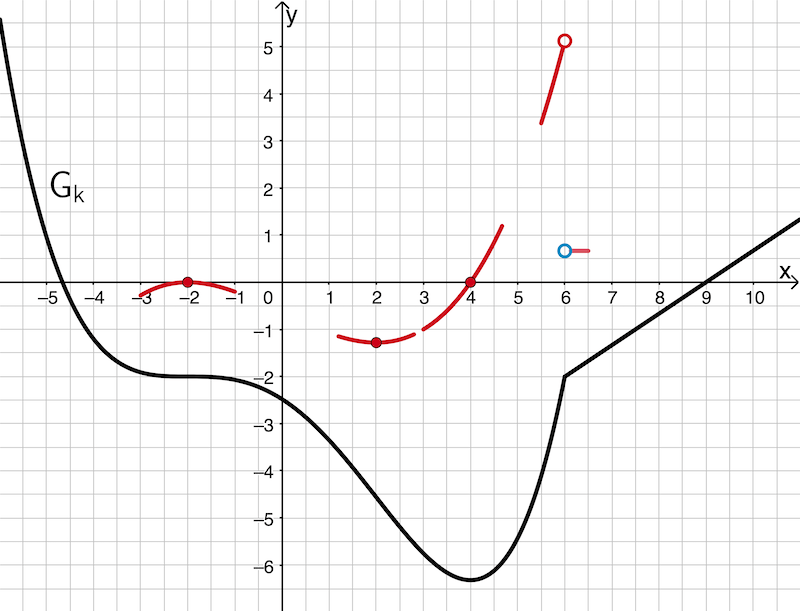
An der „Kickstelle" \(x = 6\) ist die Funktion \(k\) nicht differenzierbar („nicht ableitbar"). Der Funktionswert \(k'(6)\) existiert nicht (vgl. Teilaufgabe a). Der Graph von \(k'\) nähert sich linksseitig in etwa dem Punkt \((6|\textcolor{#cc071e}{5})\) und rechtsseitig dem Punkt \(\left(6|\textcolor{#0087c1}{\large{\frac{2}{3}}}\right)\) an.
\[\underbrace{\lim \limits_{\textcolor{#cc071e}{\underset{x \,< \,6}{x\, \to\, 6}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#cc071e}{\text{linksseitiger Grenzwert}}}} \approx \textcolor{#cc071e}{5}\]
\[\underbrace{\lim \limits_{\textcolor{#0087c1}{\underset{x \,> \,6}{x\, \to\, 6}}}\frac{k(x) - k(0)}{x - 0}}_{\large{\textcolor{#0087c1}{\text{rechtsseitiger Grenzwert}}}} = \textcolor{#0087c1}{\frac{2}{3}}\]
(vgl. Teilaufgabe a)
Verlauf des Graphen von \(\boldsymbol{k}\) für \(\boldsymbol{x \to -\infty}\) bzw. \(\boldsymbol{x \to +\infty}\)
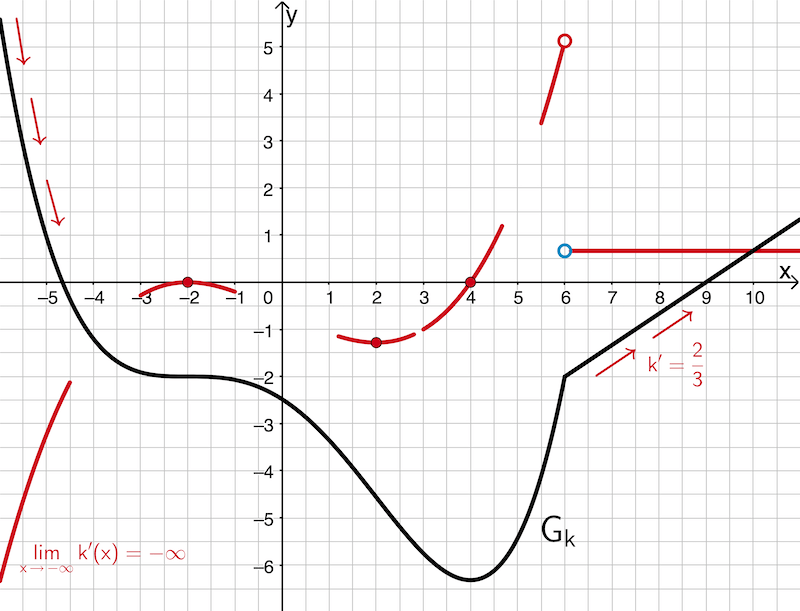
Für \(x \to -\infty\) verläuft der Graph von \(k\) steil nach \(+\infty\), weshalb die Steigung des Graphen beliebig negativ (unendlich negativ) wird. Der Graph von \(\textcolor{#cc071e}{k'}\) verläuft somit für \(x \to -\infty\) steil nach \(\textcolor{#cc071e}{-\infty}\) \(\Big(\textcolor{#cc071e}{\lim \limits_{x\,\to\,-\infty} k'(x) = -\infty}\Big)\).
Für \(x > 6\) ist der Graph von \(k\) eine Gerade mit der Steigung \(\textcolor{#cc071e}{\dfrac{2}{3}}\). Damit gilt \(\textcolor{#cc071e}{k'(x) = \dfrac{2}{3}}\) für \(x > 6\) und der Graph von \(\textcolor{#cc071e}{k'}\) zeigt für \(x \to +\infty\) den Verlauf der Gerade mit der Gleichung \(\textcolor{#cc071e}{y = \dfrac{2}{3}}\).
Zusammenfassend ergibt sich folgende Skizze:

Graph der Funktion \(k\) und Graph der Ableitungsfunktion \(\textcolor{#cc071e}{k'}\)

