Die Funktion \(\vert f(x) \vert\) wird als Betragsfunktion der Funktion \(f(x)\) bezeichnet. Betragsfunktionen können abschnittsweise beschrieben werden.

Definitionsmenge: \(D_{\vert f \vert} = D_{f}\)

Wertemenge \(W_{\vert f \vert}\): Der Betrag aller Elemente der Wertemenge \(W_{f}\) der Funktion \(f\)

 

Beispiel: \(f(x) = x\)

\[\vert f(x) \vert = \vert x \vert = \begin{cases} \hspace{13px}x &\text{für} \quad x \geq 0 \\[0.8em] -x &\text{für} \quad x < 0 \end{cases}\]

\[D_{\vert f \vert} = R\,, \enspace W_{\vert f \vert} = R_{0}^{+}\]

 

Funktionsgraph einer Betragsfunktion

Der Graph der Betragsfunktion \(\vert f(x) \vert\) entsteht aus dem Graphen der Funktion \(f(x)\), indem alle unterhalb der \(x\)-Achse verlaufenden Teile des Graphen an der \(x\)-Achse gespiegelt werden und die oberhalb der \(x\)-Achse verlaufenden Teile des Graphen beibehalten werden.

 

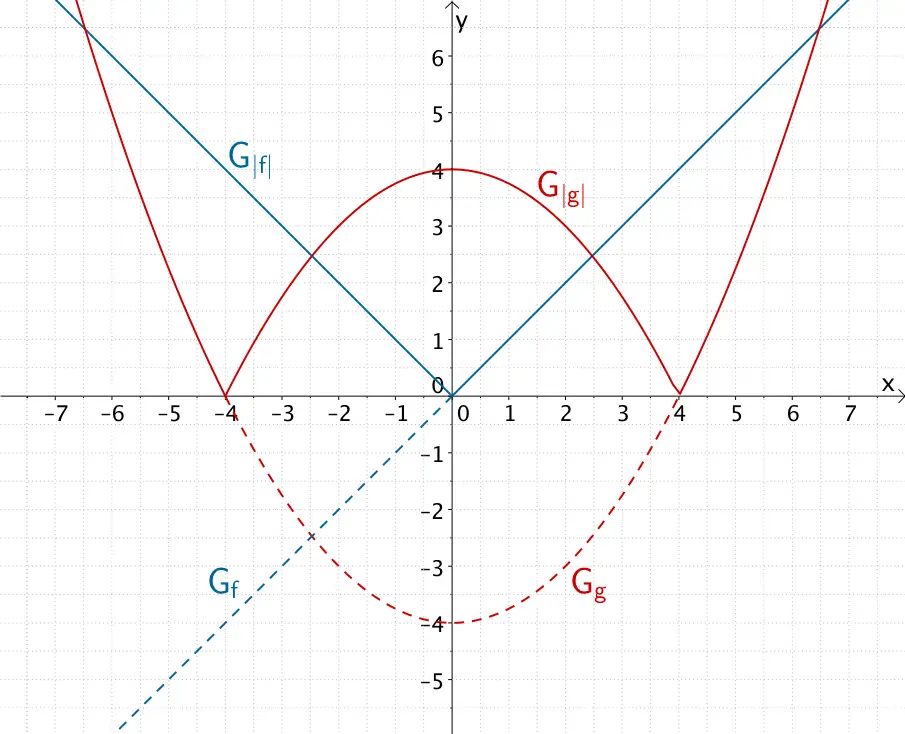
Graphen der Betragsfunktionen \(\vert f(x) \vert = \vert x \vert\) und \(\vert g(x) \vert = \vert \dfrac{1}{4}x^{2} - 4\vert\)

 

Differenzierbarkeit einer Betragsfunktion

Die Betragsfunktion \(\vert f(x) \vert\) einer in \(D_{f}\) differenzierbaren Funktion \(f\) ist an den einfachen Nullstellen der Funktion \(f\) („Knickstellen" des Graphen der Betragsfunktion) nicht differenzierbar (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit).

 

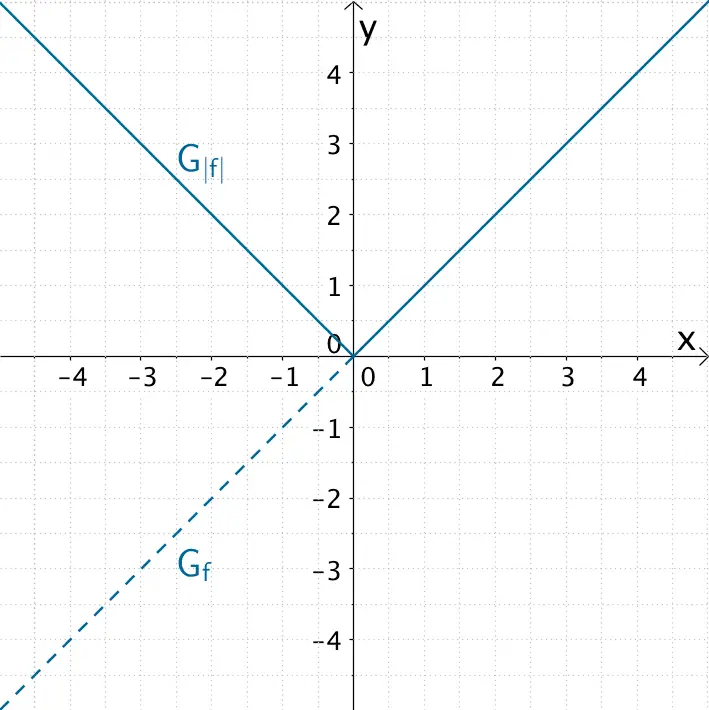
Die Betragsfunktion \(\vert f(x) \vert\) ist an der einfachen Nullstelle \(x = 0\) der Funktion \(f\colon x \mapsto x\) nicht differenzierbar (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit).

 

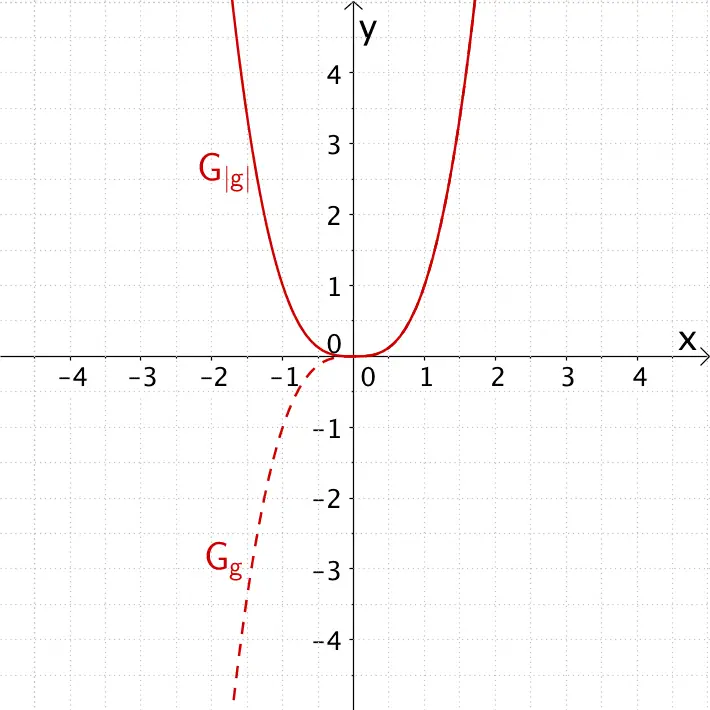
Die Betragsfunktion \(\vert g(x)\vert\) ist an der dreifachen Nullstelle \(x = 0\) der Funktion \(g\colon x \mapsto x^{3}\) differenzierbar (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit).

 

Betragsgleichungen

Im Rahmen der abiturrelevanten Mathematik beschränkt sich dieser Abschnitt auf die Betrachtung einfacher linearer Betragsgleichungen.

Beispielsweise führt das Lösen einer reinquadratischen Gleichung der Form \(x^{2} - c = 0\) mit \(c \in \mathbb R_{0}^{+}\) auf eine lineare Betragsgleichung.

Aus der Schulmathematik ist folgende Kurzschreibweise bekannt:

 

\[\begin{align*}x^{2} - c &= 0 &&| + c \\[0.8em] x^{2} &= c &&| \; \sqrt{\quad} \enspace (c \in \mathbb R_{0}^{+}) \\[0.8em] x_{1,2} &= \pm \sqrt{c}\end{align*}\]

 

Da eine Wurzel mit Ausnahme von \(\sqrt{0} = 0\) immer ein positives Ergebnis liefert (vgl. Abiturskript - 1.1.4 Wurzelfunktion, Wertebereich), gilt \(\sqrt{x^{2}} = \vert x \vert\) und somit lautet die ausführliche Schreibweise:

 

\[\begin{align*}x^{2} - c &= 0 &&| + c \\[0.8em] x^{2} &= c &&| \; \sqrt{\quad} \enspace (c \in \mathbb R_{0}^{+}) \\[0.8em] \sqrt{x^{2}} &= \sqrt{c} \\[0.8em] \vert x \vert &= \sqrt{c}\end{align*}\]

 

Mit \(\vert x \vert = \begin{cases} \hspace{13px}x &\text{für} \quad x \geq 0 \\[0.8em] -x &\text{für} \quad x < 0 \end{cases}\) ergibt sich folgende Fallunterscheidung:

 

1. Fall: \(x \geq 0\)

Für \(x \geq 0\) können die Betragsstriche von \(\vert x \vert\) entfallen.

 

\[\Rightarrow \enspace x = \sqrt{c}\]

 

2. Fall: \(x < 0\)

Für \(x < 0\) ersetzt \(-x\) den Term \(\vert x \vert\).

 

\[\begin{align*}\Rightarrow \enspace -x &= \sqrt{c} &&| \cdot (-1) \\[0.8em] x &= -\sqrt{c}\end{align*}\]

 

Also lauten die Lösungen \(x_{1} = -\sqrt{c}\) und \(x_{2} = +\sqrt{c}\).

 

Analog lassen sich durch eine derartige Fallunterscheidung lineare Betragsgleichungen der Form \(\vert ax + b \vert = c\) mit \(a \neq 0\) und \(b,c \in \mathbb R\) lösen.

 

1. Fall: \(ax + b \textcolor{#0087c1}{\geq} 0\)

Die Betragsstriche des Terms \(\vert ax + b \vert\) können entfallen.

Es ist die Gleichung \(ax + b = c\) zu lösen.

 

2. Fall: \(ax +b \textcolor{#cc071e}{<} 0\)

Die Vorzeichenänderung \(\textcolor{#cc071e}{-(}ax + b\textcolor{#cc071e}{)}\) ersetzt den Betrag des Terms \(\vert ax + b \vert\).

Es ist die Gleichung \(-(ax + b) = c\) zu lösen.

 

Beispiel: \(\vert -3x + 2 \vert = 4\)

 

1. Fall: \(-3x + 2 \textcolor{#0087c1}{\geq} 0\)

Die Betragsstriche des Terms \(\vert -3x + 2 \vert\) können entfallen.

Es ist die Gleichung \(-3x + 2 = 4\) zu lösen.

 

\[\begin{align*} -3x + 2 &= 4 &&| -2 \\[0.8em] -3x &= 2 &&| : (-3) \\[0.8em] x &= -\frac{2}{3} \end{align*}\]

 

2. Fall: \(-3x + 2 \textcolor{#cc071e}{<} 0\)

Die Vorzeichenänderung \(\textcolor{#cc071e}{-(}-3x + 2\textcolor{#cc071e}{)}\) ersetzt den Betrag des Terms \(\vert -3x + 2 \vert\).

Es ist die Gleichung \(-(-3x + 2) = 4\) zu lösen.

 

\[\begin{align*} -(-3x + 2) &= 4 \\[0.8em] 3x - 2 &= 4 &&| + 2 \\[0.8em] 3x &= 6 &&| : 3 \\[0.8em] x &= 2 \end{align*}\]

 

Die lineare Betragsgleichung \(\vert -3x + 2 \vert = 4\) hat also die Lösungen \(x_{1} = -\frac{2}{3}\) und \(x_{2} = 2\).

 

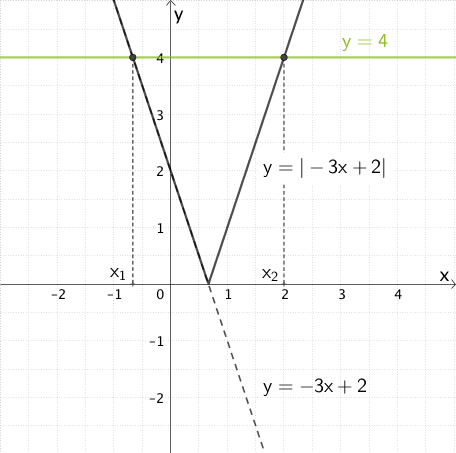
 Graphische Lösung der linearen Betragsgleichung \(\vert -3x + 2\vert = \textcolor{#89ba17}{4}\)

 

Beispielaufgabe

Geben Sie den Funktionsterm einer in \(\mathbb R\) definierten und an den Stellen \(x = -2\) sowie \(x = 2\) nicht differenzierbaren Funktion \(f\) an.

 

\[g(x) = (x - 2)(x + 2) = x^{2} + 4\,; \enspace D = \mathbb R\]

 

Die Funktion \(g\) besitzt die beiden einfachen Nullstellen \(x = -2\) und \(x = 2\). Die Betragsfunktion der Funktion \(g\) ist an den einfachen Nullstellen der Funktion \(g\) („Knickstellen" des Graphen der Betragsfunktion) nicht differenzierbar (vgl. Abiturskript - 1.5.1 Die Ableitung, Differenzierbarkeit).

 

\[\Longrightarrow \quad f(x) = \vert g(x) \vert = \vert x^{2} - 4 \vert\,; \enspace D = \mathbb R\,, \enspace W = \mathbb R_{0}^{+}\]

 

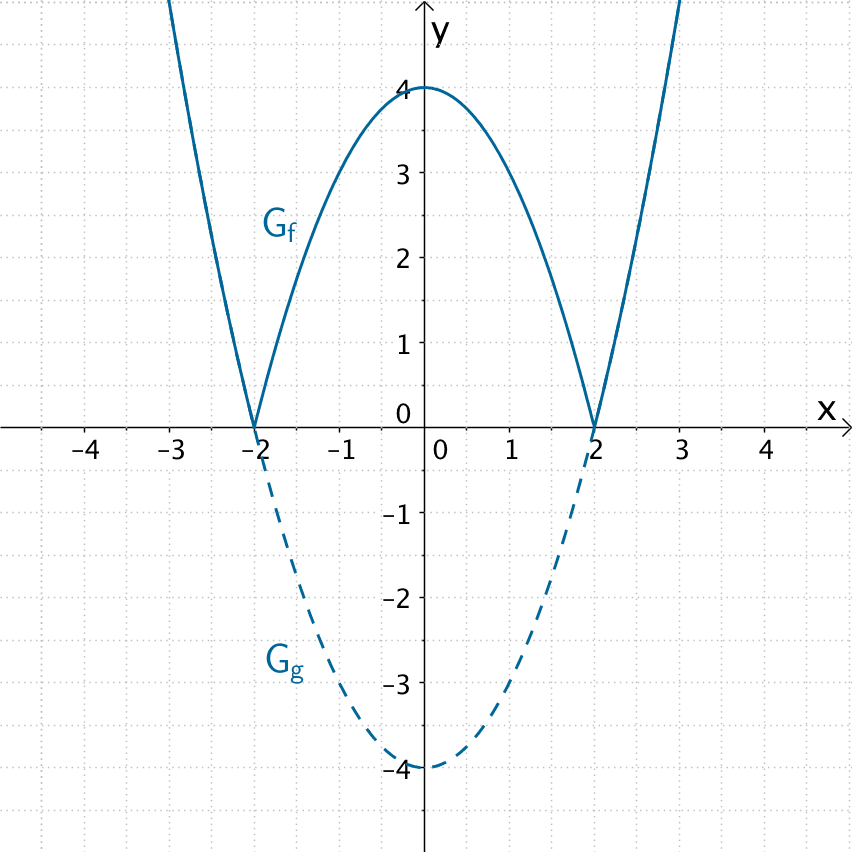
Graph der Betragsfunktion \(f\colon x \mapsto \vert x^{2} - 4 \vert\)