Die Zufallsgröße \(X\) beschreibt, wie oft der Mechanismus beim Schließen des Vorhangs im Verlauf einer Aufführung nicht funktioniert. Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Wert von \(X\) um mehr als eine Standardabweichung vom Erwartungswert der Zufallsgröße abweicht.
(5 BE)
Lösung zu Teilaufgabe 4c
Binomialverteilung
Zufallsgröße \(X \colon \enspace\) "Anzahl der Defekte des automatischen Mechanismus"
Aus Teilaufgabe 4a ist bekannt:
\(n = 15\,, \enspace p = 0{,}1\)
Die Zufallsgröße \(X\) ist nach \(B(15;0{,}1)\) binomialverteilt.
Die Standardabweichung ist ein Maß dafür, wie stark die zu erwartenden Werte einer Zufallsgröße um den Erwartungswert streuen. In dieser Aufgabe soll die Wahrscheinlichkeit dafür bestimmt werden, dass die Werte der Zufallsgröße \(X\) außerhalb der durch die Standardabweichung festgelegten Streuung liegen.
Gesucht: \(\;P^{15}_{0{,}1}(X < \mu - \sigma \; \vee \; X > \mu + \sigma)\)
Erwartungswert der Zufallsgröße \(X\) bestimmen:
Erwartungswert \(\boldsymbol{\mu}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\(\mu = E(X) = n \cdot p\) (vgl. Merkhilfe)
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist.
\[\mu = E(X) = n \cdot p = 15 \cdot 0{,}1 = 1{,}5\]
Standardabweichung der Zufallsgröße \(X\) bestimmen:
Standardabweichung \(\boldsymbol{\sigma}\) einer binomialverteilten Zufallsgröße \(\boldsymbol{X}\)
\[\sigma = \sqrt{Var(X)} = \sqrt{n \cdot p \cdot (1 - p)}\]
Wobei \(n\) die Länge der Bernoullikette und \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses ist. \(Var(X)\) bezeichnet die Varianz der Zufallsgröße \(X\).
\[\sigma = \sqrt{n \cdot p \cdot (1 - p)} = \sqrt{15 \cdot 0{,}1 \cdot (1 - 0{,}1)} = \sqrt{1{,}35} \approx 1{,}16\]
Streugrenzen der Sigma-Umgebung bestimmen:
\[\mu - \sigma = 1{,}5 - \sqrt{1{,}35} \approx 0{,}34\]
\[\mu - \sigma = 1{,}5 + \sqrt{1{,}35} \approx 2{,}66\]
Wahrscheinlichkeit \(\,P^{15}_{0{,}1}(X < \mu - \sigma \; \vee \; X > \mu + \sigma)\,\) berechnen:
\[\begin{align*}P^{15}_{0{,}1}(X < \mu - \sigma \; \vee \; X > \mu + \sigma) &= P^{15}_{0{,}1}(X < 0{,}34 \, \vee \, X > 2{,}66) \\[0.8em] &= P^{15}_{0{,}1}(X = 0 \, \vee \, X \geq 3) \\[0.8em] &= P^{15}_{0{,}1}(X = 0) + P^{15}_{0{,}1}(X \geq 3) & &| \;\text{Gegenereignis betrachten} \\[0.8em] &= P^{15}_{0{,}1}(X = 0) + 1 - P^{15}_{0{,}1}(X \leq 2) \end{align*}\]
Stochastisches Tafelwerk (ST) verwenden:
Kumulative Verteilungsfunktion einer nach \(B(n, p)\) binomialverteilten Zufallsgröße \(X\)
\[F^n_p (k) = P^n_p (X \leq k) = \sum_{i \, = \, 0}^k B(n; p; i) = \sum_{i \, = \, 0}^k \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i}\]
Wobei \(n\) die Länge der Bernoullikette, \(p\) die Trefferwahrscheinlichkeit für das Eintreten des betrachteten Ereignisses und \(k \in \{0,1,\dots,n\}\) die Anzahl der Treffer ist.
Das Stochastische Tafelwerk (ST) listet die Werte der Kumulativen Verteilungsfunktion jeweils in der rechten Spalte einer betrachteten Tabelle der Parameter \(n\) und \(p\).
\[\begin{align*}P^{15}_{0{,}1}(X < \mu - \sigma \; \vee \; X > \mu + \sigma) &= P^{15}_{0{,}1}(X = 0) + 1 - P^{15}_{0{,}1}(X \leq 2) \\[0.8em] &\overset{ST}{=} 0{,}20589 + 1 - 0{,}81594 \\[0.8em] &= 0{,}38995 \approx 39\,\% \end{align*}\]
Alternative: Rechenweg mit dem Gegenereignis beginnen
\[\begin{align*}P^{15}_{0{,}1}(X < \mu - \sigma \; \vee \; X > \mu + \sigma) &= 1 - P^{15}_{0{,}1}(\mu - \sigma \leq X \leq \mu + \sigma) \\[0.8em] &= 1 - P^{15}_{0{,}1}(0{,}34 \leq X \leq 2{,}66) \\[0.8em] &= 1 - P^{15}_{0{,}1}(1 \leq X \leq 2) \\[0.8em] &= 1 - \big[ P^{15}_{0{,}1}(X = 1) + P^{15}_{0{,}1}(X = 2) \big] \\[0.8em] &\overset{ST}{=} 1 - (0{,}34315 + 0{,}26690) \\[0.8em] &= 0{,}38995 \approx 39\,\% \end{align*}\]
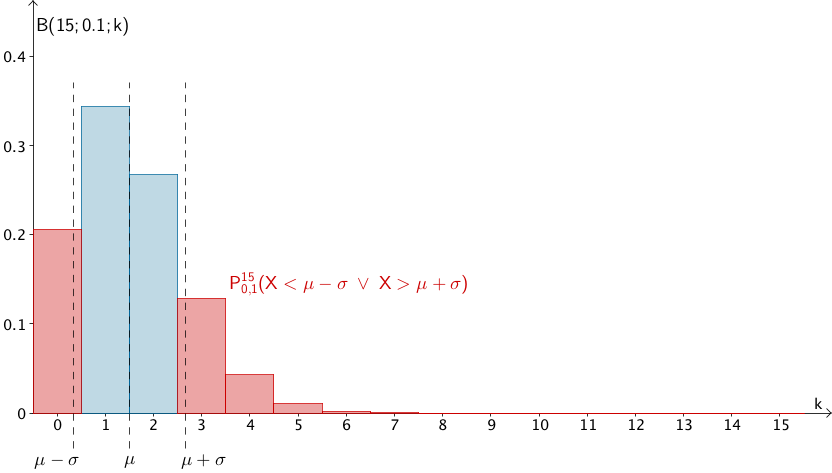
Wahrscheinlichkeitsverteilung dafür, dass der Wert der Zufallsgröße \(\,X\,\) um mehr als eine Standardabweichung \(\,\sigma\,\) vom Erwartungswert \(\,\mu\,\) der Zufallsgröße abweicht.


